Causal Interpretation of Self-Attention in Pre-Trained Transformers

We propose a causal interpretation of self-attention in the Transformer neural network architecture. We interpret self-attention as a mechanism that estimates a structural equation model for a given input sequence of symbols (tokens). The structural equation model can be interpreted, in turn, as a causal structure over the input symbols under the specific context of the input sequence. Importantly, this interpretation remains valid in the presence of latent confounders. Following this interpretation, we estimate conditional independence relations between input symbols by calculating partial correlations between their corresponding representations in the deepest attention layer. This enables learning the causal structure over an input sequence using existing constraint-based algorithms. In this sense, existing pre-trained Transformers can be utilized for zero-shot causal-discovery. We demonstrate this method by providing causal explanations for the outcomes of Transformers in two tasks: sentiment classification (NLP) and recommendation.

From Temporal to Contemporaneous Iterative Causal Discovery in the Presence of Latent Confounders

We present a constraint-based algorithm for learning causal structures from observational time-series data, in the presence of latent confounders. We assume a discrete-time, stationary structural vector autoregressive process, with both temporal and contemporaneous causal relations. One may ask if temporal and contemporaneous relations should be treated differently. The presented algorithm gradually refines a causal graph by learning long-term temporal relations before short-term ones, where contemporaneous relations are learned last. This ordering of causal relations to be learnt leads to a reduction in the required number of statistical tests. We validate this reduction empirically and demonstrate that it leads to higher accuracy for synthetic data and more plausible causal graphs for real-world data compared to state-of-the-art algorithms.

Iterative Causal Discovery in the Possible Presence of Latent Confounders and Selection Bias

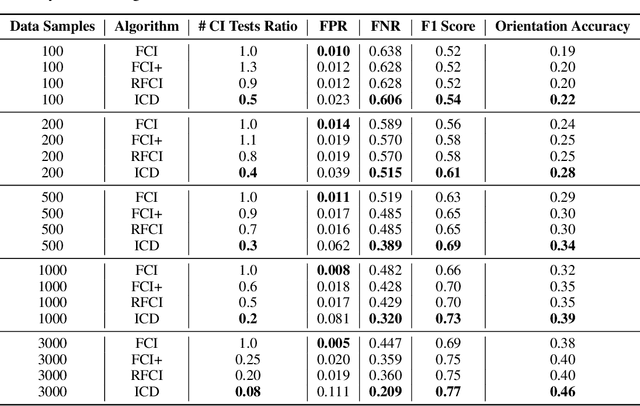
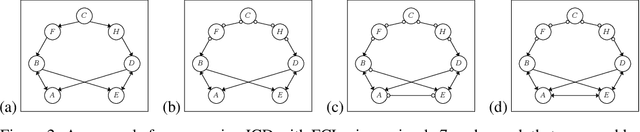
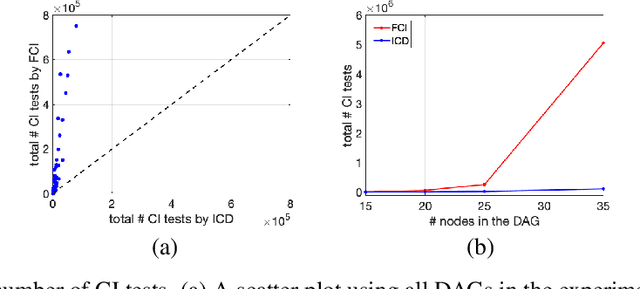
We present a sound and complete algorithm, called iterative causal discovery (ICD), for recovering causal graphs in the presence of latent confounders and selection bias. ICD relies on the causal Markov and faithfulness assumptions and recovers the equivalence class of the underlying causal graph. It starts with a complete graph, and consists of a single iterative stage that gradually refines this graph by identifying conditional independence (CI) between connected nodes. Independence and causal relations entailed after any iteration are correct, rendering ICD anytime. Essentially, we tie the size of the CI conditioning set to its distance on the graph from the tested nodes, and increase this value in the successive iteration. Thus, each iteration refines a graph that was recovered by previous iterations having smaller conditioning sets -- a higher statistical power -- which contributes to stability. We demonstrate empirically that ICD requires significantly fewer CI tests and learns more accurate causal graphs compared to FCI, FCI+, and RFCI algorithms.

Improving Efficiency and Accuracy of Causal Discovery Using a Hierarchical Wrapper

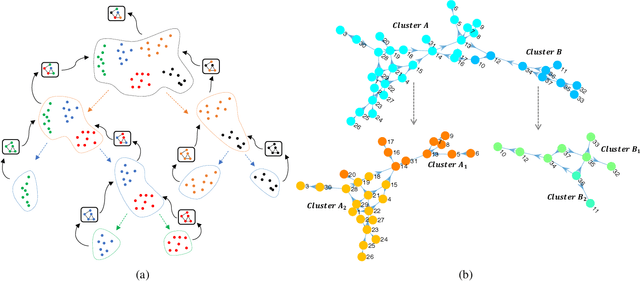
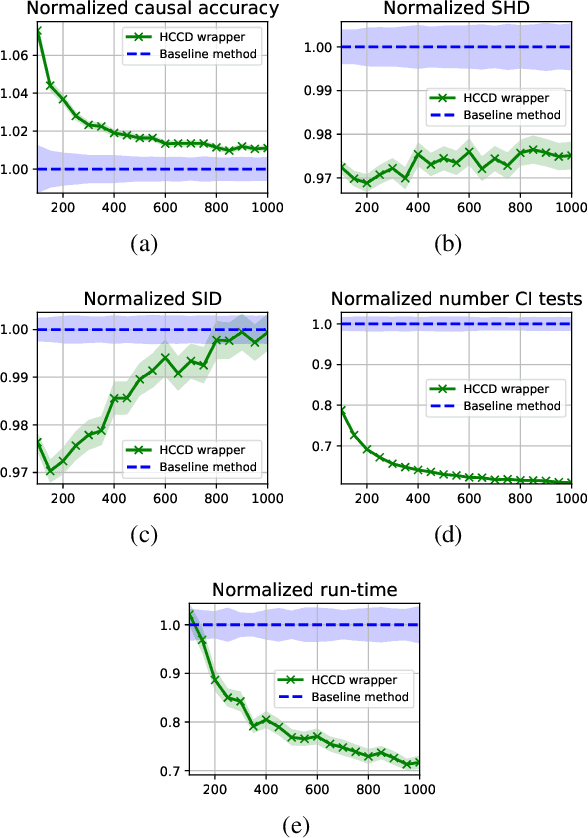
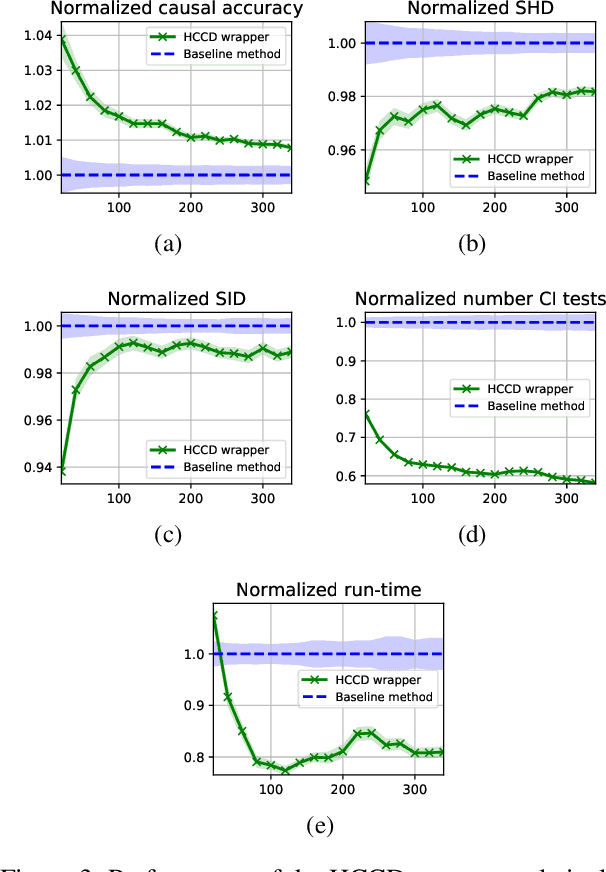
Causal discovery from observational data is an important tool in many branches of science. Under certain assumptions it allows scientists to explain phenomena, predict, and make decisions. In the large sample limit, sound and complete causal discovery algorithms have been previously introduced, where a directed acyclic graph (DAG), or its equivalence class, representing causal relations is searched. However, in real-world cases, only finite training data is available, which limits the power of statistical tests used by these algorithms, leading to errors in the inferred causal model. This is commonly addressed by devising a strategy for using as few as possible statistical tests. In this paper, we introduce such a strategy in the form of a recursive wrapper for existing constraint-based causal discovery algorithms, which preserves soundness and completeness. It recursively clusters the observed variables using the normalized min-cut criterion from the outset, and uses a baseline causal discovery algorithm during backtracking for learning local sub-graphs. It then combines them and ensures completeness. By an ablation study, using synthetic data, and by common real-world benchmarks, we demonstrate that our approach requires significantly fewer statistical tests, learns more accurate graphs, and requires shorter run-times than the baseline algorithm.

A Single Iterative Step for Anytime Causal Discovery

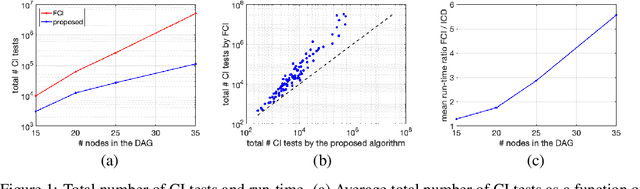
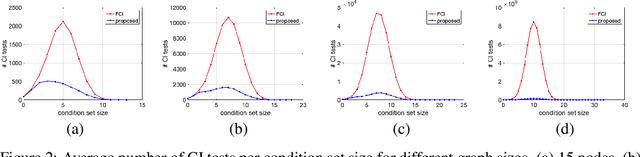
We present a sound and complete algorithm for recovering causal graphs from observed, non-interventional data, in the possible presence of latent confounders and selection bias. We rely on the causal Markov and faithfulness assumptions and recover the equivalence class of the underlying causal graph by performing a series of conditional independence (CI) tests between observed variables. We propose a single step that is applied iteratively, such that the independence and causal relations entailed from the resulting graph, after any iteration, is correct and becomes more informative with successive iteration. Essentially, we tie the size of the CI condition set to its distance from the tested nodes on the resulting graph. Each iteration refines the skeleton and orientation by performing CI tests having condition sets that are larger than in the preceding iteration. In an iteration, condition sets of CI tests are constructed from nodes that are within a specified search distance, and the sizes of these condition sets is equal to this search distance. The algorithm then iteratively increases the search distance along with the condition set sizes. Thus, each iteration refines a graph, that was recovered by previous iterations having smaller condition sets -- having a higher statistical power. We demonstrate that our algorithm requires significantly fewer CI tests and smaller condition sets compared to the FCI algorithm. This is evident for both recovering the true underlying graph using a perfect CI oracle, and accurately estimating the graph using limited observed data.

Modeling Uncertainty by Learning a Hierarchy of Deep Neural Connections

Quantifying and measuring uncertainty in deep neural networks, despite recent important advances, is still an open problem. Bayesian neural networks are a powerful solution, where the prior over network weights is a design choice, often a normal distribution or other distribution encouraging sparsity. However, this prior is agnostic to the generative process of the input data, which might lead to unwarranted generalization for out-of-distribution tested data. We suggest treating the generative process of the input data as a confounder for the relation between the input and the discriminative function, thereby conditioning the prior of the network weights on the distribution of the input. We propose an algorithm for modeling this confounder through neural connectivity patterns. This approach is ultimately translated into a new deep architecture---a compact hierarchy of networks. We demonstrate that sampling networks from this hierarchy, proportionally to their posterior, is efficient and enables estimating various types of uncertainties. Empirical evaluations of our method demonstrate significant improvement compared to state-of-the-art calibration and out-of-distribution detection methods.

Constructing Deep Neural Networks by Bayesian Network Structure Learning

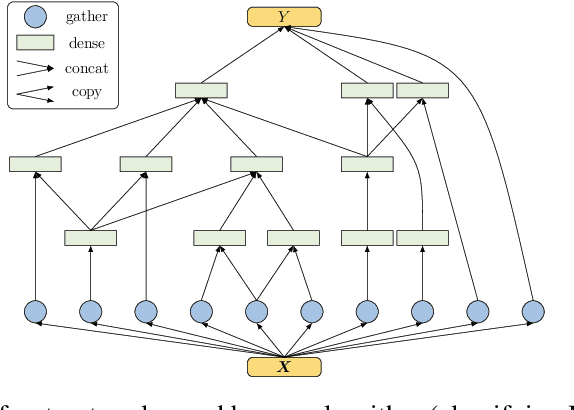
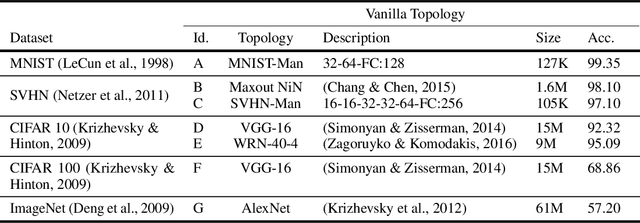
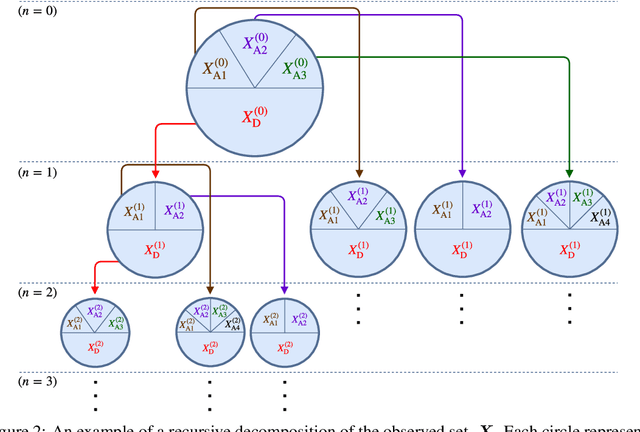
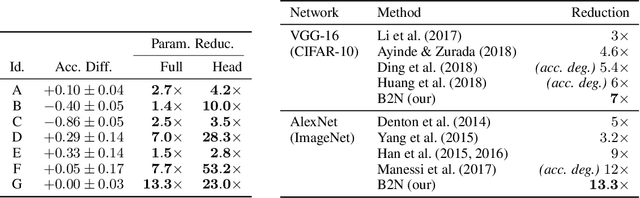
We introduce a principled approach for unsupervised structure learning of deep neural networks. We propose a new interpretation for depth and inter-layer connectivity where conditional independencies in the input distribution are encoded hierarchically in the network structure. Thus, the depth of the network is determined inherently. The proposed method casts the problem of neural network structure learning as a problem of Bayesian network structure learning. Then, instead of directly learning the discriminative structure, it learns a generative graph, constructs its stochastic inverse, and then constructs a discriminative graph. We prove that conditional-dependency relations among the latent variables in the generative graph are preserved in the class-conditional discriminative graph. We demonstrate on image classification benchmarks that the deepest layers (convolutional and dense) of common networks can be replaced by significantly smaller learned structures, while maintaining classification accuracy---state-of-the-art on tested benchmarks. Our structure learning algorithm requires a small computational cost and runs efficiently on a standard desktop CPU.

Bayesian Structure Learning by Recursive Bootstrap

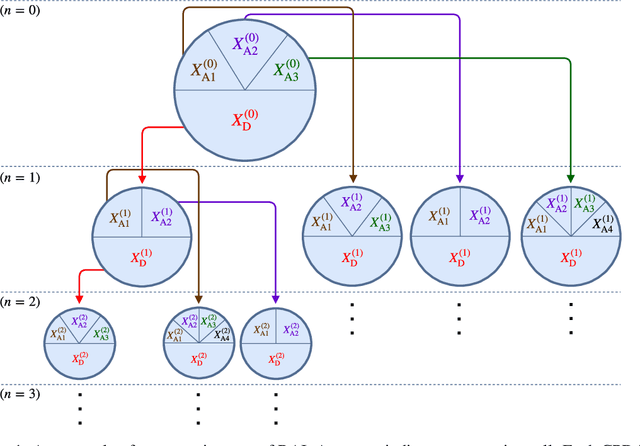
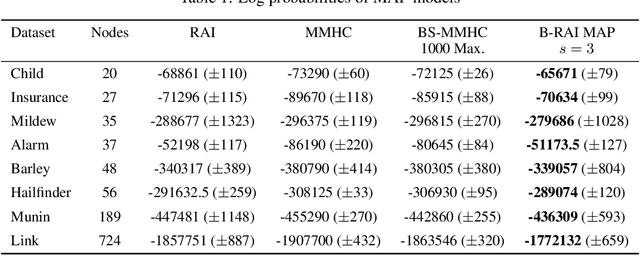
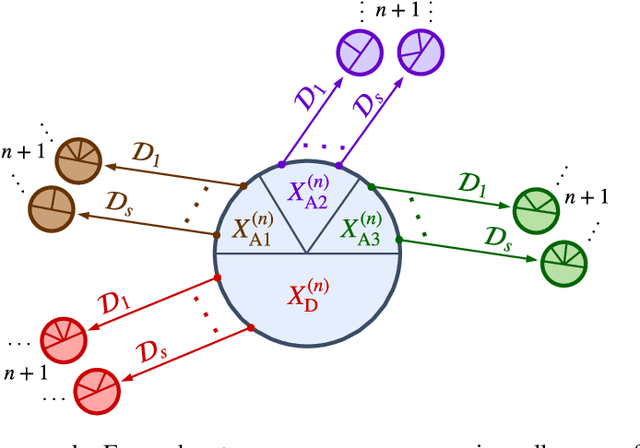
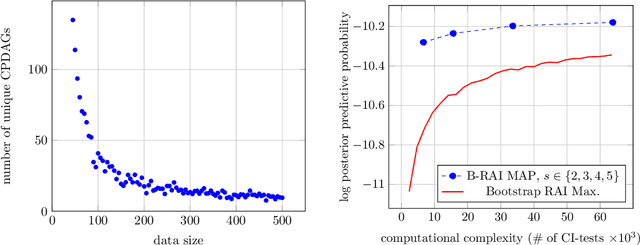
We address the problem of Bayesian structure learning for domains with hundreds of variables by employing non-parametric bootstrap, recursively. We propose a method that covers both model averaging and model selection in the same framework. The proposed method deals with the main weakness of constraint-based learning---sensitivity to errors in the independence tests---by a novel way of combining bootstrap with constraint-based learning. Essentially, we provide an algorithm for learning a tree, in which each node represents a scored CPDAG for a subset of variables and the level of the node corresponds to the maximal order of conditional independencies that are encoded in the graph. As higher order independencies are tested in deeper recursive calls, they benefit from more bootstrap samples, and therefore more resistant to the curse-of-dimensionality. Moreover, the re-use of stable low order independencies allows greater computational efficiency. We also provide an algorithm for sampling CPDAGs efficiently from their posterior given the learned tree. We empirically demonstrate that the proposed algorithm scales well to hundreds of variables, and learns better MAP models and more reliable causal relationships between variables, than other state-of-the-art-methods.