Constructing Deep Neural Networks by Bayesian Network Structure Learning

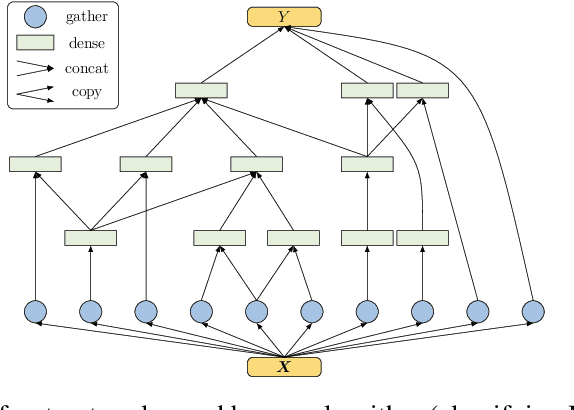
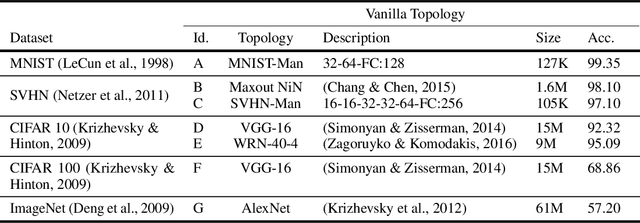
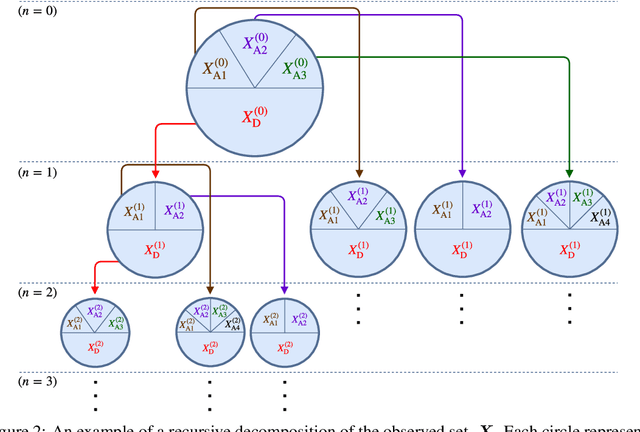
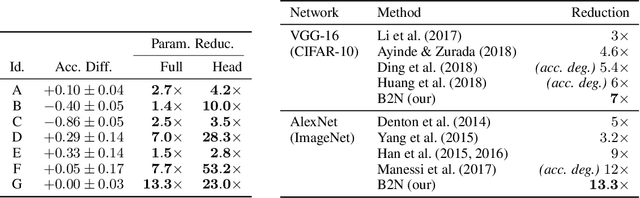
We introduce a principled approach for unsupervised structure learning of deep neural networks. We propose a new interpretation for depth and inter-layer connectivity where conditional independencies in the input distribution are encoded hierarchically in the network structure. Thus, the depth of the network is determined inherently. The proposed method casts the problem of neural network structure learning as a problem of Bayesian network structure learning. Then, instead of directly learning the discriminative structure, it learns a generative graph, constructs its stochastic inverse, and then constructs a discriminative graph. We prove that conditional-dependency relations among the latent variables in the generative graph are preserved in the class-conditional discriminative graph. We demonstrate on image classification benchmarks that the deepest layers (convolutional and dense) of common networks can be replaced by significantly smaller learned structures, while maintaining classification accuracy---state-of-the-art on tested benchmarks. Our structure learning algorithm requires a small computational cost and runs efficiently on a standard desktop CPU.

Bayesian Structure Learning by Recursive Bootstrap

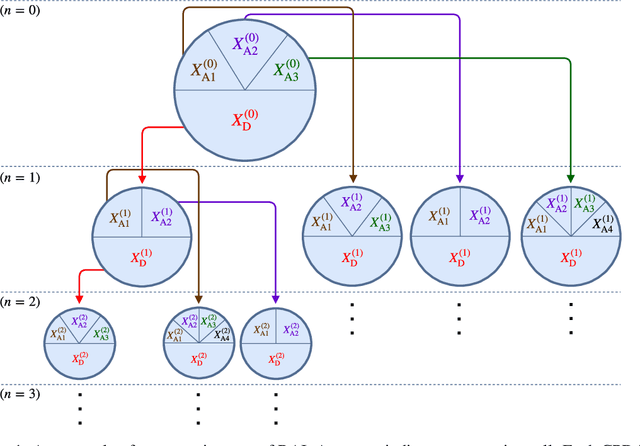
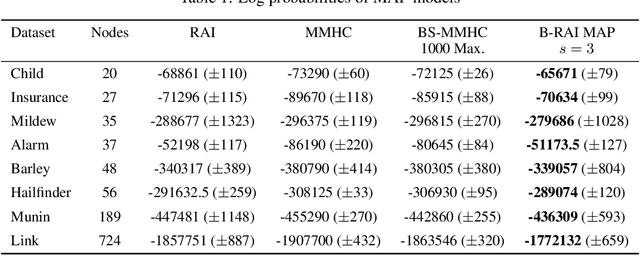
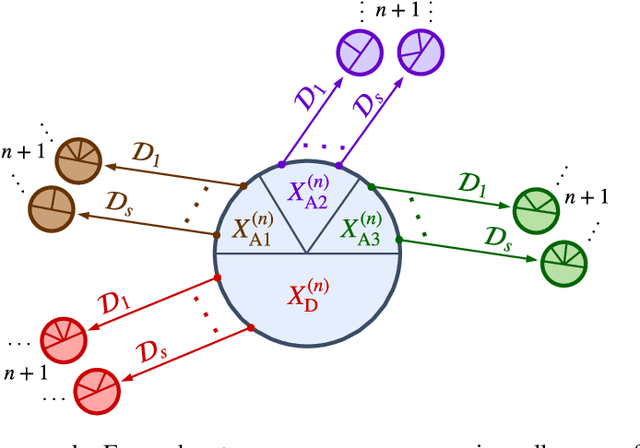
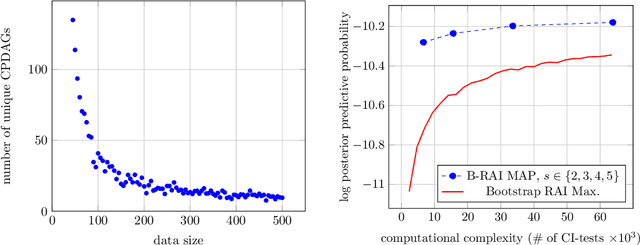
We address the problem of Bayesian structure learning for domains with hundreds of variables by employing non-parametric bootstrap, recursively. We propose a method that covers both model averaging and model selection in the same framework. The proposed method deals with the main weakness of constraint-based learning---sensitivity to errors in the independence tests---by a novel way of combining bootstrap with constraint-based learning. Essentially, we provide an algorithm for learning a tree, in which each node represents a scored CPDAG for a subset of variables and the level of the node corresponds to the maximal order of conditional independencies that are encoded in the graph. As higher order independencies are tested in deeper recursive calls, they benefit from more bootstrap samples, and therefore more resistant to the curse-of-dimensionality. Moreover, the re-use of stable low order independencies allows greater computational efficiency. We also provide an algorithm for sampling CPDAGs efficiently from their posterior given the learned tree. We empirically demonstrate that the proposed algorithm scales well to hundreds of variables, and learns better MAP models and more reliable causal relationships between variables, than other state-of-the-art-methods.