Constructing Deep Neural Networks by Bayesian Network Structure Learning
Paper and Code
Oct 17, 2018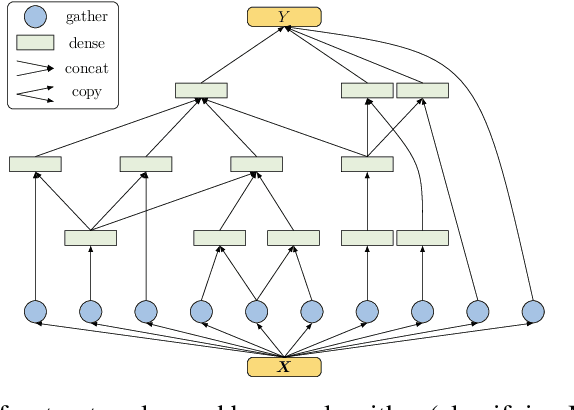
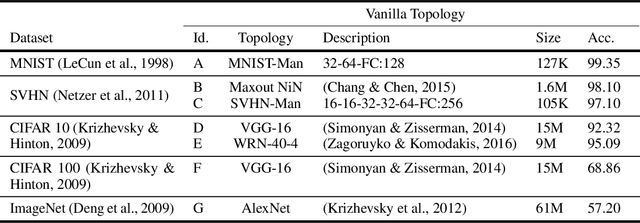
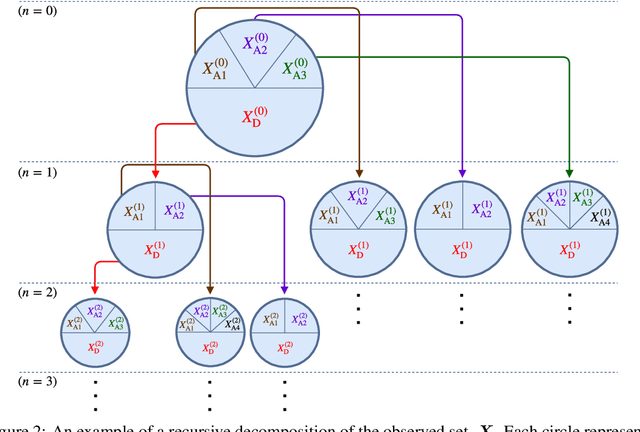
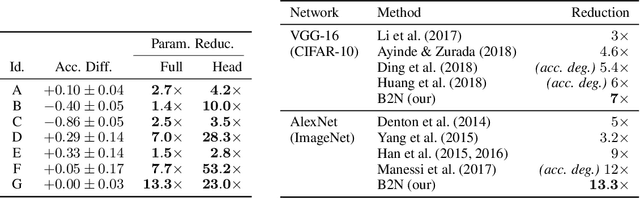
We introduce a principled approach for unsupervised structure learning of deep neural networks. We propose a new interpretation for depth and inter-layer connectivity where conditional independencies in the input distribution are encoded hierarchically in the network structure. Thus, the depth of the network is determined inherently. The proposed method casts the problem of neural network structure learning as a problem of Bayesian network structure learning. Then, instead of directly learning the discriminative structure, it learns a generative graph, constructs its stochastic inverse, and then constructs a discriminative graph. We prove that conditional-dependency relations among the latent variables in the generative graph are preserved in the class-conditional discriminative graph. We demonstrate on image classification benchmarks that the deepest layers (convolutional and dense) of common networks can be replaced by significantly smaller learned structures, while maintaining classification accuracy---state-of-the-art on tested benchmarks. Our structure learning algorithm requires a small computational cost and runs efficiently on a standard desktop CPU.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge