Bayesian Structure Learning by Recursive Bootstrap
Paper and Code
Sep 13, 2018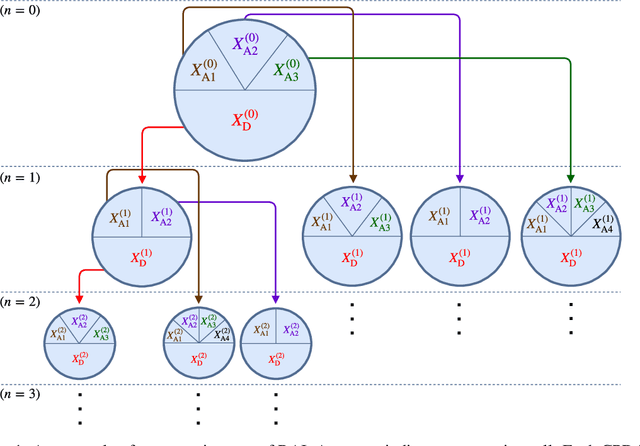
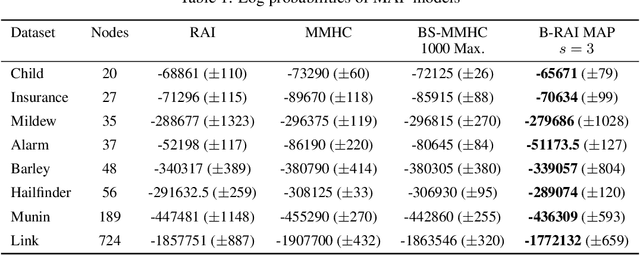
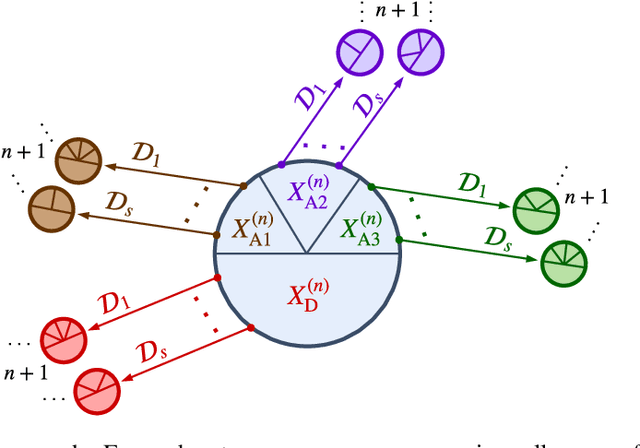
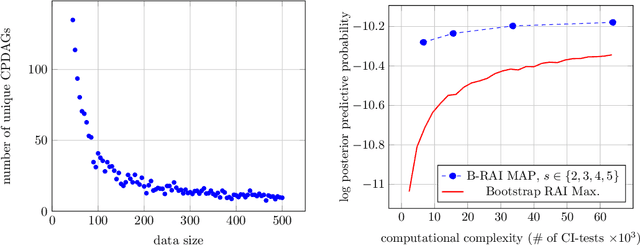
We address the problem of Bayesian structure learning for domains with hundreds of variables by employing non-parametric bootstrap, recursively. We propose a method that covers both model averaging and model selection in the same framework. The proposed method deals with the main weakness of constraint-based learning---sensitivity to errors in the independence tests---by a novel way of combining bootstrap with constraint-based learning. Essentially, we provide an algorithm for learning a tree, in which each node represents a scored CPDAG for a subset of variables and the level of the node corresponds to the maximal order of conditional independencies that are encoded in the graph. As higher order independencies are tested in deeper recursive calls, they benefit from more bootstrap samples, and therefore more resistant to the curse-of-dimensionality. Moreover, the re-use of stable low order independencies allows greater computational efficiency. We also provide an algorithm for sampling CPDAGs efficiently from their posterior given the learned tree. We empirically demonstrate that the proposed algorithm scales well to hundreds of variables, and learns better MAP models and more reliable causal relationships between variables, than other state-of-the-art-methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge