A Single Iterative Step for Anytime Causal Discovery
Paper and Code
Dec 24, 2020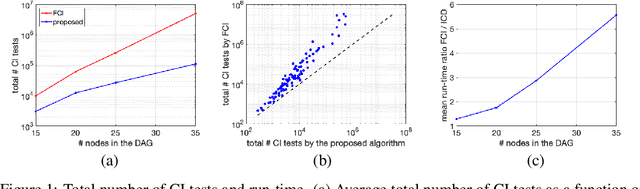
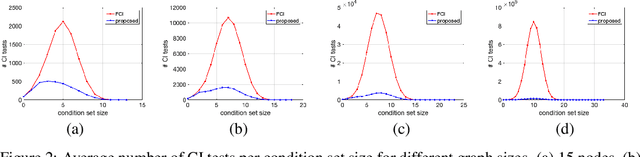
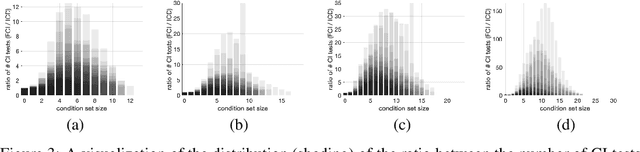
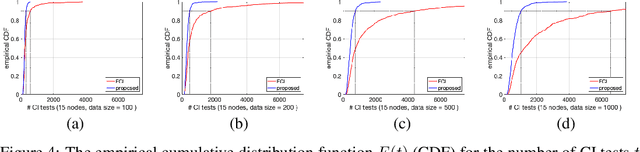
We present a sound and complete algorithm for recovering causal graphs from observed, non-interventional data, in the possible presence of latent confounders and selection bias. We rely on the causal Markov and faithfulness assumptions and recover the equivalence class of the underlying causal graph by performing a series of conditional independence (CI) tests between observed variables. We propose a single step that is applied iteratively, such that the independence and causal relations entailed from the resulting graph, after any iteration, is correct and becomes more informative with successive iteration. Essentially, we tie the size of the CI condition set to its distance from the tested nodes on the resulting graph. Each iteration refines the skeleton and orientation by performing CI tests having condition sets that are larger than in the preceding iteration. In an iteration, condition sets of CI tests are constructed from nodes that are within a specified search distance, and the sizes of these condition sets is equal to this search distance. The algorithm then iteratively increases the search distance along with the condition set sizes. Thus, each iteration refines a graph, that was recovered by previous iterations having smaller condition sets -- having a higher statistical power. We demonstrate that our algorithm requires significantly fewer CI tests and smaller condition sets compared to the FCI algorithm. This is evident for both recovering the true underlying graph using a perfect CI oracle, and accurately estimating the graph using limited observed data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge