Modeling Uncertainty by Learning a Hierarchy of Deep Neural Connections

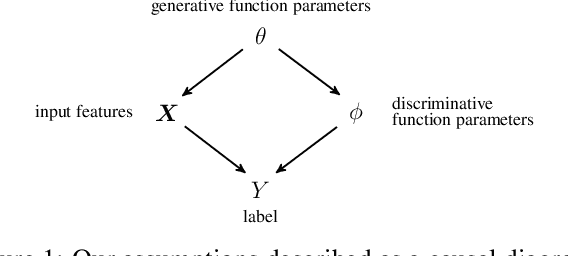
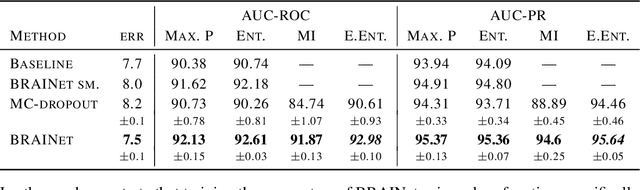
Quantifying and measuring uncertainty in deep neural networks, despite recent important advances, is still an open problem. Bayesian neural networks are a powerful solution, where the prior over network weights is a design choice, often a normal distribution or other distribution encouraging sparsity. However, this prior is agnostic to the generative process of the input data, which might lead to unwarranted generalization for out-of-distribution tested data. We suggest treating the generative process of the input data as a confounder for the relation between the input and the discriminative function, thereby conditioning the prior of the network weights on the distribution of the input. We propose an algorithm for modeling this confounder through neural connectivity patterns. This approach is ultimately translated into a new deep architecture---a compact hierarchy of networks. We demonstrate that sampling networks from this hierarchy, proportionally to their posterior, is efficient and enables estimating various types of uncertainties. Empirical evaluations of our method demonstrate significant improvement compared to state-of-the-art calibration and out-of-distribution detection methods.