NeuralPLexer3: Accurate Biomolecular Complex Structure Prediction with Flow Models

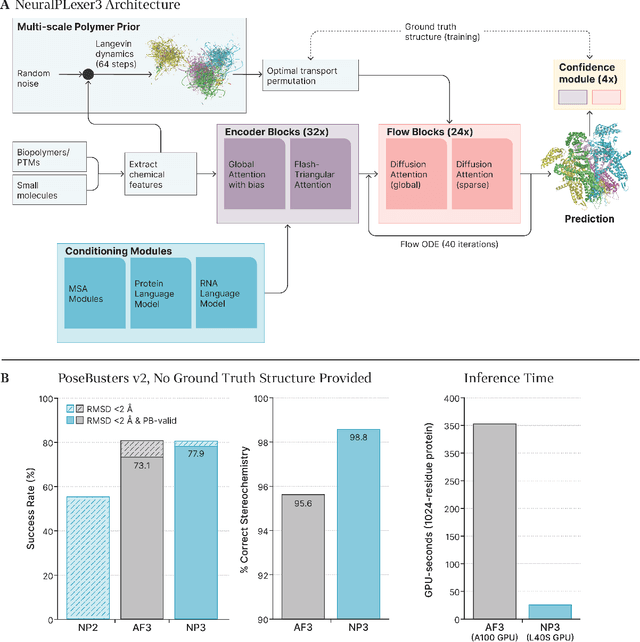
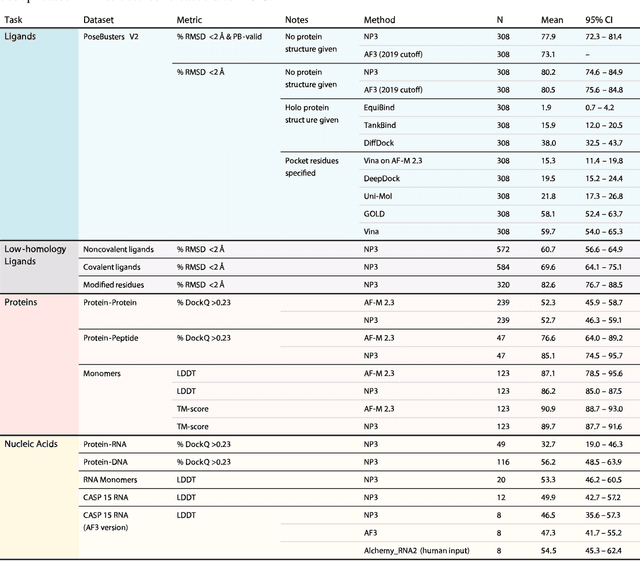
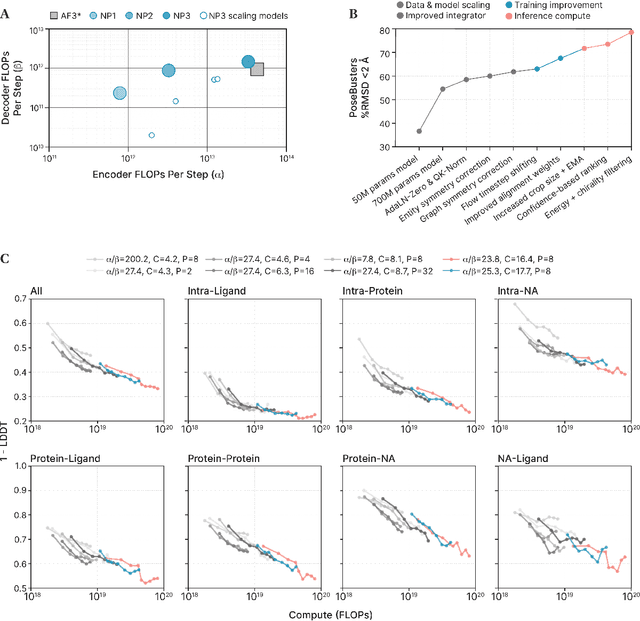
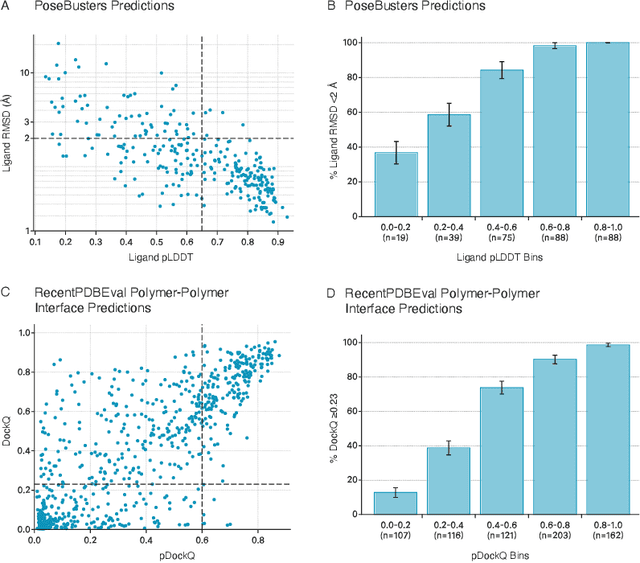
Structure determination is essential to a mechanistic understanding of diseases and the development of novel therapeutics. Machine-learning-based structure prediction methods have made significant advancements by computationally predicting protein and bioassembly structures from sequences and molecular topology alone. Despite substantial progress in the field, challenges remain to deliver structure prediction models to real-world drug discovery. Here, we present NeuralPLexer3 -- a physics-inspired flow-based generative model that achieves state-of-the-art prediction accuracy on key biomolecular interaction types and improves training and sampling efficiency compared to its predecessors and alternative methodologies. Examined through newly developed benchmarking strategies, NeuralPLexer3 excels in vital areas that are crucial to structure-based drug design, such as physical validity and ligand-induced conformational changes.

UNiTE: Unitary N-body Tensor Equivariant Network with Applications to Quantum Chemistry

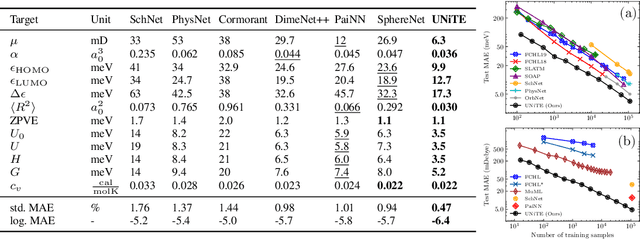
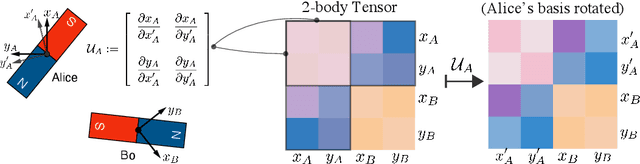
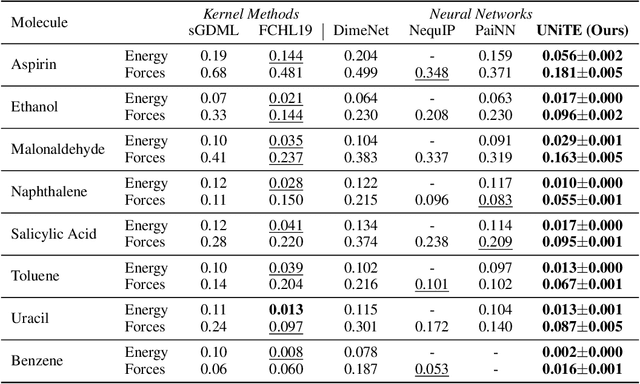
Equivariant neural networks have been successful in incorporating various types of symmetries, but are mostly limited to vector representations of geometric objects. Despite the prevalence of higher-order tensors in various application domains, e.g. in quantum chemistry, equivariant neural networks for general tensors remain unexplored. Previous strategies for learning equivariant functions on tensors mostly rely on expensive tensor factorization which is not scalable when the dimensionality of the problem becomes large. In this work, we propose unitary $N$-body tensor equivariant neural network (UNiTE), an architecture for a general class of symmetric tensors called $N$-body tensors. The proposed neural network is equivariant with respect to the actions of a unitary group, such as the group of 3D rotations. Furthermore, it has a linear time complexity with respect to the number of non-zero elements in the tensor. We also introduce a normalization method, viz., Equivariant Normalization, to improve generalization of the neural network while preserving symmetry. When applied to quantum chemistry, UNiTE outperforms all state-of-the-art machine learning methods of that domain with over 110% average improvements on multiple benchmarks. Finally, we show that UNiTE achieves a robust zero-shot generalization performance on diverse down stream chemistry tasks, while being three orders of magnitude faster than conventional numerical methods with competitive accuracy.

Multi-task learning for electronic structure to predict and explore molecular potential energy surfaces

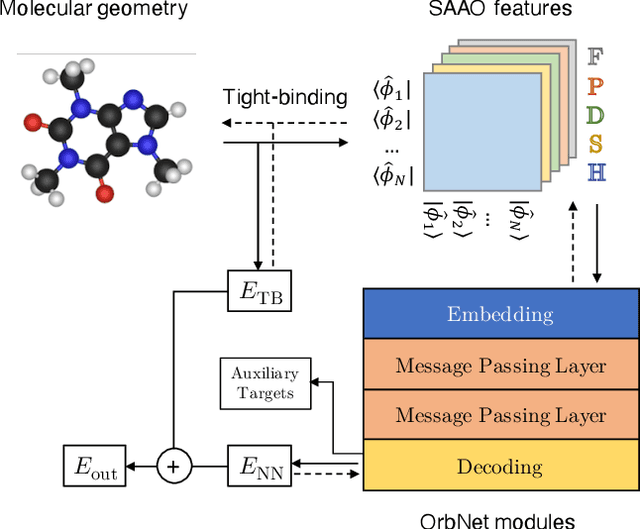
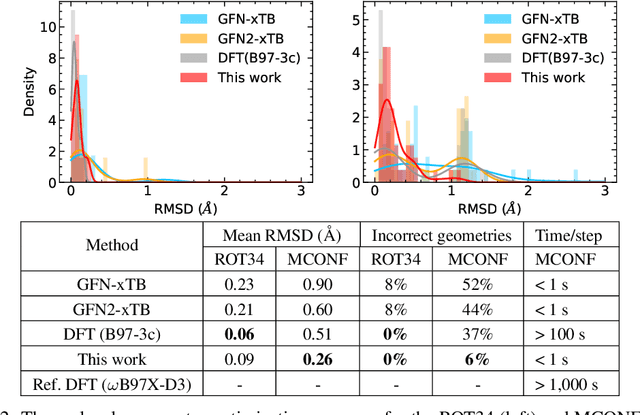
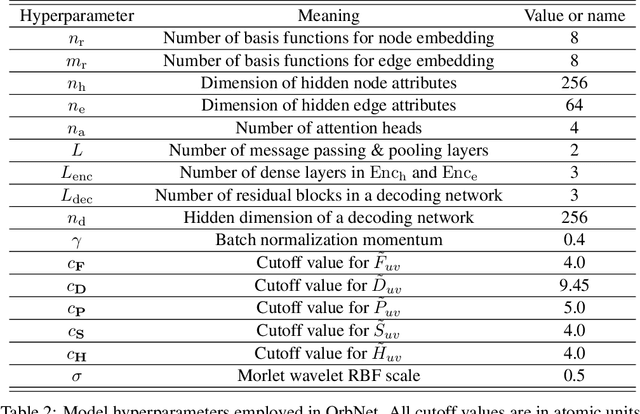
We refine the OrbNet model to accurately predict energy, forces, and other response properties for molecules using a graph neural-network architecture based on features from low-cost approximated quantum operators in the symmetry-adapted atomic orbital basis. The model is end-to-end differentiable due to the derivation of analytic gradients for all electronic structure terms, and is shown to be transferable across chemical space due to the use of domain-specific features. The learning efficiency is improved by incorporating physically motivated constraints on the electronic structure through multi-task learning. The model outperforms existing methods on energy prediction tasks for the QM9 dataset and for molecular geometry optimizations on conformer datasets, at a computational cost that is thousand-fold or more reduced compared to conventional quantum-chemistry calculations (such as density functional theory) that offer similar accuracy.

OrbNet: Deep Learning for Quantum Chemistry Using Symmetry-Adapted Atomic-Orbital Features

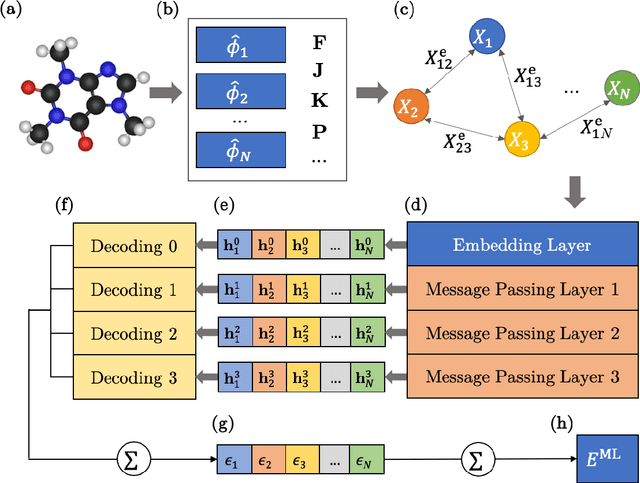
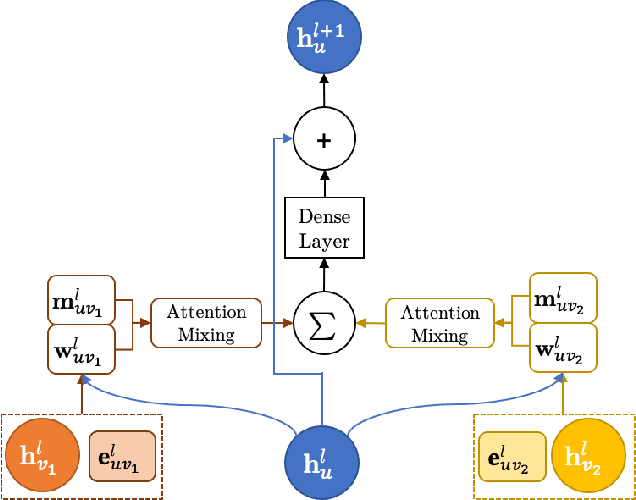
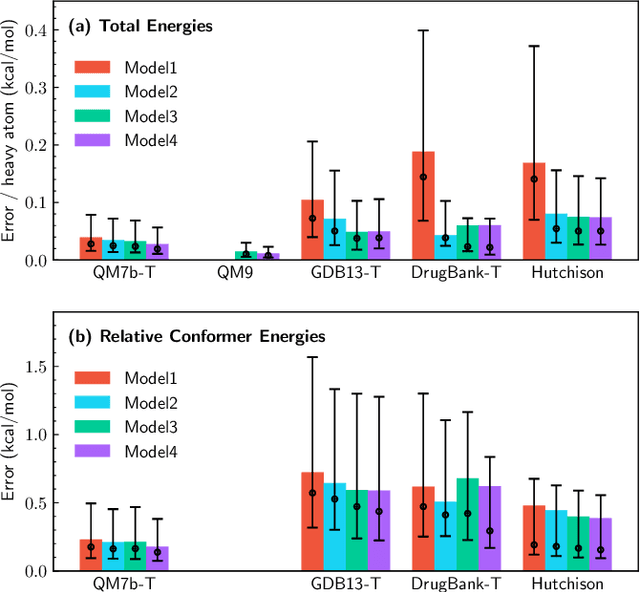
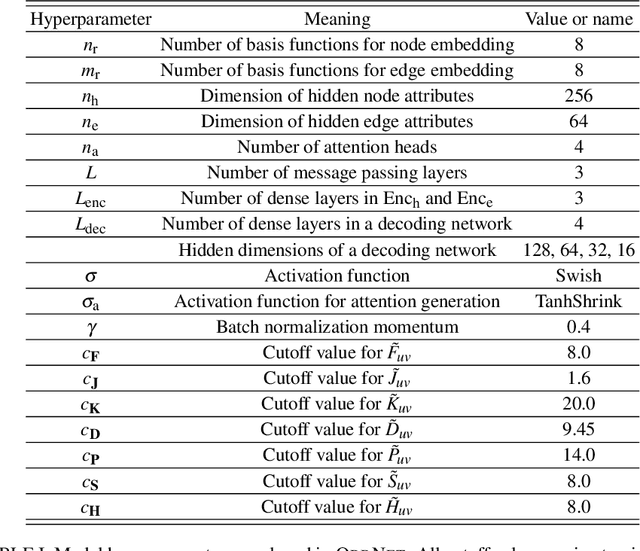
We introduce a machine learning method in which energy solutions from the Schrodinger equation are predicted using symmetry adapted atomic orbitals features and a graph neural-network architecture. \textsc{OrbNet} is shown to outperform existing methods in terms of learning efficiency and transferability for the prediction of density functional theory results while employing low-cost features that are obtained from semi-empirical electronic structure calculations. For applications to datasets of drug-like molecules, including QM7b-T, QM9, GDB-13-T, DrugBank, and the conformer benchmark dataset of Folmsbee and Hutchison, \textsc{OrbNet} predicts energies within chemical accuracy of DFT at a computational cost that is thousand-fold or more reduced.