Sharp Threshold for the Frechet Mean of Inhomogeneous Erdos-Renyi Random Graphs

We address the following foundational question: what is the population, and sample, Frechet mean (or median) graph of an ensemble of inhomogeneous Erdos-Renyi random graphs? We prove that if we use the Hamming distance to compute distances between graphs, then the Frechet mean (or median) graph of an ensemble of inhomogeneous random graphs is obtained by thresholding the expected adjacency matrix of the ensemble. We show that the result also holds for the sample mean (or median) when the population expected adjacency matrix is replaced with the sample mean adjacency matrix. Consequently, the Frechet mean (or median) graph of inhomogeneous Erdos-Renyi random graphs exhibits a sharp threshold: it is either the empty graph, or the complete graph. This novel theoretical result has some significant practical consequences; for instance, the Frechet mean of an ensemble of sparse inhomogeneous random graphs is always the empty graph.

Theoretical analysis and computation of the sample Frechet mean for sets of large graphs based on spectral information

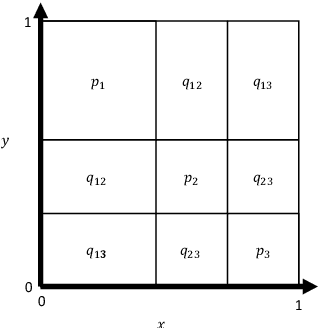
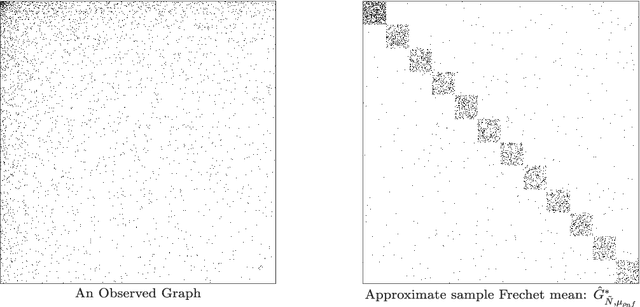
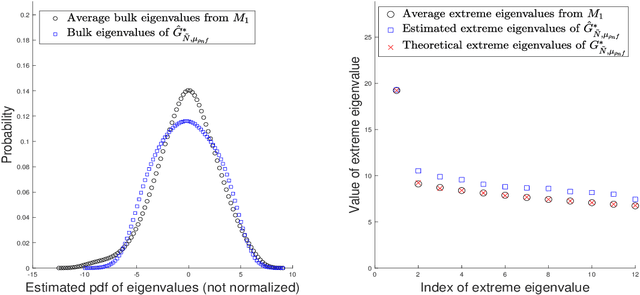
To characterize the location (mean, median) of a set of graphs, one needs a notion of centrality that is adapted to metric spaces, since graph sets are not Euclidean spaces. A standard approach is to consider the Frechet mean. In this work, we equip a set of graphs with the pseudometric defined by the norm between the eigenvalues of their respective adjacency matrix. Unlike the edit distance, this pseudometric reveals structural changes at multiple scales, and is well adapted to studying various statistical problems for graph-valued data. We describe an algorithm to compute an approximation to the sample Frechet mean of a set of undirected unweighted graphs with a fixed size using this pseudometric.

The Sample Fréchet Mean of Sparse Graphs is Sparse

The availability of large datasets composed of graphs creates an unprecedented need to invent novel tools in statistical learning for "graph-valued random variables". To characterize the "average" of a sample of graphs, one can compute the sample Fr\'echet mean. Because the sample mean should provide an interpretable summary of the graph sample, one would expect that the structural properties of the sample be transmitted to the Fr\'echet mean. In this paper, we address the following foundational question: does the sample Fr\'echet mean inherit the structural properties of the graphs in the sample? Specifically, we prove the following result: the sample Fr\'echet mean of a set of sparse graphs is sparse. We prove the result for the graph Hamming distance, and the spectral adjacency pseudometric, using very different arguments. In fact, we prove a stronger result: the edge density of the sample Fr\'echet mean is bounded by the edge density of the graphs in the sample. This result guarantees that sparsity is an hereditary property, which can be transmitted from a graph sample to its sample Fr\'echet mean, irrespective of the method used to estimate the sample Fr\'echet mean.

Non-Asymptotic Analysis of Tangent Space Perturbation

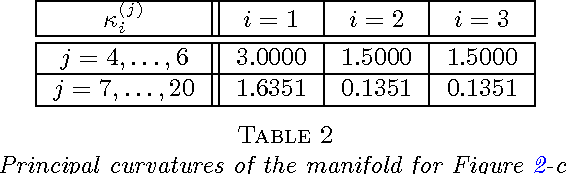
Constructing an efficient parameterization of a large, noisy data set of points lying close to a smooth manifold in high dimension remains a fundamental problem. One approach consists in recovering a local parameterization using the local tangent plane. Principal component analysis (PCA) is often the tool of choice, as it returns an optimal basis in the case of noise-free samples from a linear subspace. To process noisy data samples from a nonlinear manifold, PCA must be applied locally, at a scale small enough such that the manifold is approximately linear, but at a scale large enough such that structure may be discerned from noise. Using eigenspace perturbation theory and non-asymptotic random matrix theory, we study the stability of the subspace estimated by PCA as a function of scale, and bound (with high probability) the angle it forms with the true tangent space. By adaptively selecting the scale that minimizes this bound, our analysis reveals an appropriate scale for local tangent plane recovery. We also introduce a geometric uncertainty principle quantifying the limits of noise-curvature perturbation for stable recovery. With the purpose of providing perturbation bounds that can be used in practice, we propose plug-in estimates that make it possible to directly apply the theoretical results to real data sets.

Inverting Nonlinear Dimensionality Reduction with Scale-Free Radial Basis Function Interpolation

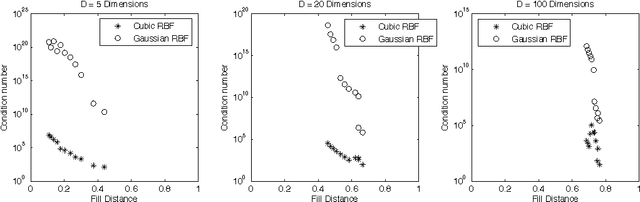
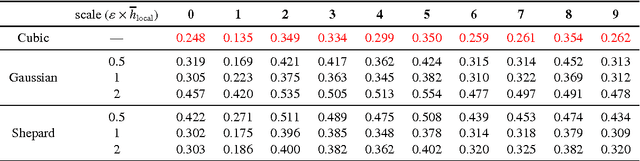
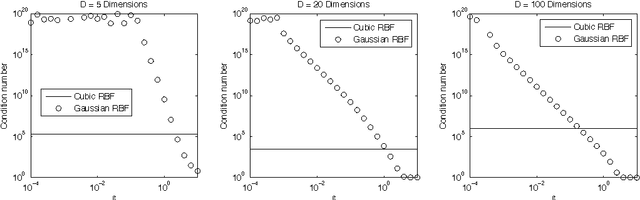
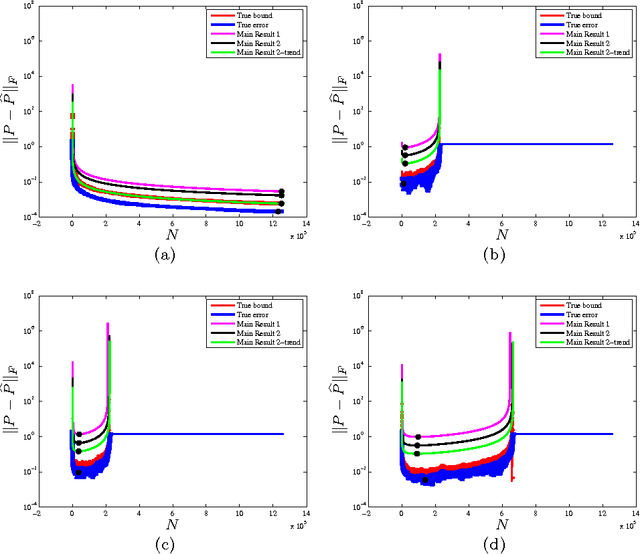
Nonlinear dimensionality reduction embeddings computed from datasets do not provide a mechanism to compute the inverse map. In this paper, we address the problem of computing a stable inverse map to such a general bi-Lipschitz map. Our approach relies on radial basis functions (RBFs) to interpolate the inverse map everywhere on the low-dimensional image of the forward map. We demonstrate that the scale-free cubic RBF kernel performs better than the Gaussian kernel: it does not suffer from ill-conditioning, and does not require the choice of a scale. The proposed construction is shown to be similar to the Nystr\"om extension of the eigenvectors of the symmetric normalized graph Laplacian matrix. Based on this observation, we provide a new interpretation of the Nystr\"om extension with suggestions for improvement.

Perturbation of the Eigenvectors of the Graph Laplacian: Application to Image Denoising

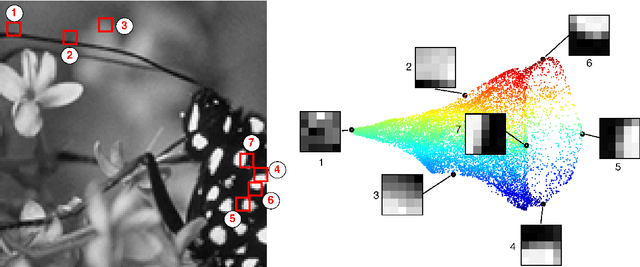
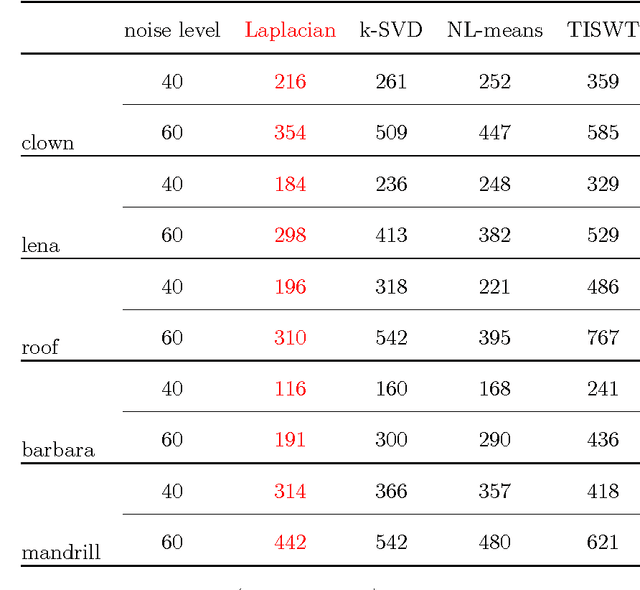
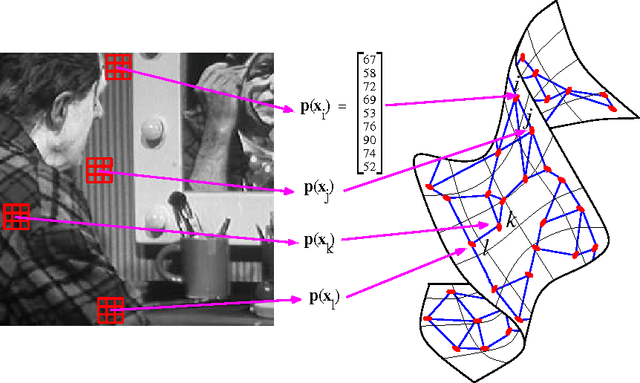
The original contributions of this paper are twofold: a new understanding of the influence of noise on the eigenvectors of the graph Laplacian of a set of image patches, and an algorithm to estimate a denoised set of patches from a noisy image. The algorithm relies on the following two observations: (1) the low-index eigenvectors of the diffusion, or graph Laplacian, operators are very robust to random perturbations of the weights and random changes in the connections of the patch-graph; and (2) patches extracted from smooth regions of the image are organized along smooth low-dimensional structures in the patch-set, and therefore can be reconstructed with few eigenvectors. Experiments demonstrate that our denoising algorithm outperforms the denoising gold-standards.

A random walk on image patches

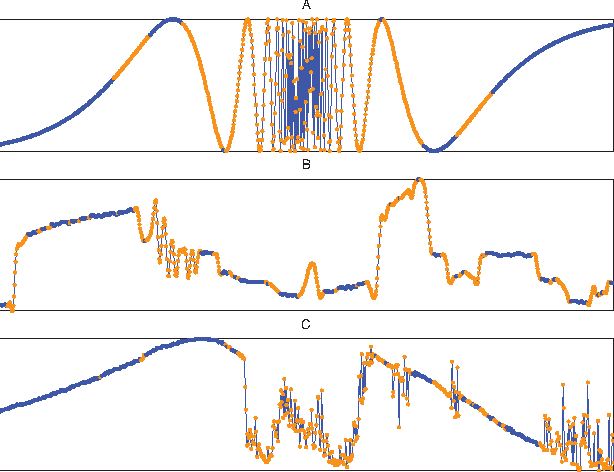
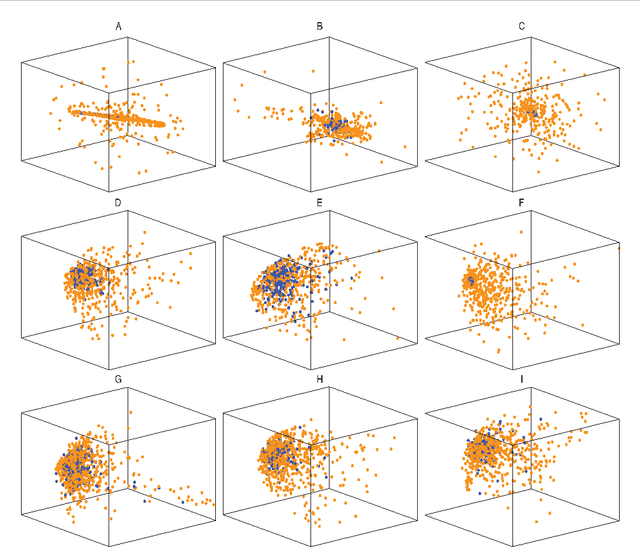
In this paper we address the problem of understanding the success of algorithms that organize patches according to graph-based metrics. Algorithms that analyze patches extracted from images or time series have led to state-of-the art techniques for classification, denoising, and the study of nonlinear dynamics. The main contribution of this work is to provide a theoretical explanation for the above experimental observations. Our approach relies on a detailed analysis of the commute time metric on prototypical graph models that epitomize the geometry observed in general patch graphs. We prove that a parametrization of the graph based on commute times shrinks the mutual distances between patches that correspond to rapid local changes in the signal, while the distances between patches that correspond to slow local changes expand. In effect, our results explain why the parametrization of the set of patches based on the eigenfunctions of the Laplacian can concentrate patches that correspond to rapid local changes, which would otherwise be shattered in the space of patches. While our results are based on a large sample analysis, numerical experimentations on synthetic and real data indicate that the results hold for datasets that are very small in practice.

Locality and low-dimensions in the prediction of natural experience from fMRI

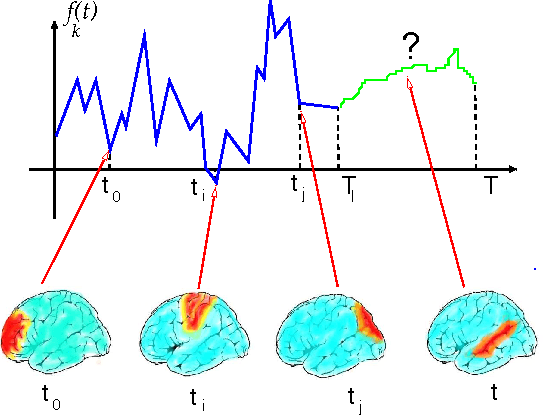
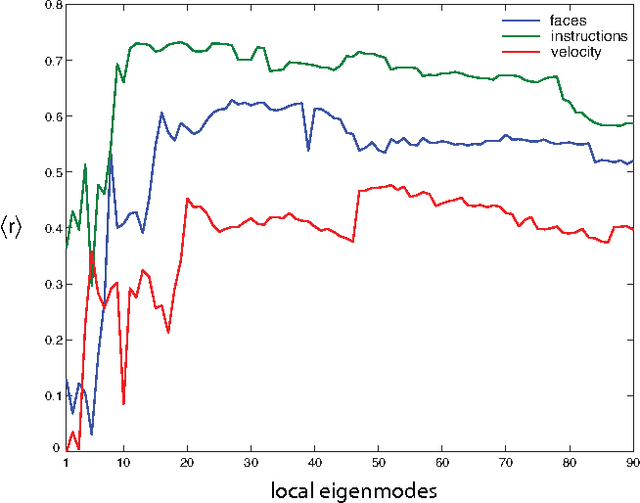
Functional Magnetic Resonance Imaging (fMRI) provides dynamical access into the complex functioning of the human brain, detailing the hemodynamic activity of thousands of voxels during hundreds of sequential time points. One approach towards illuminating the connection between fMRI and cognitive function is through decoding; how do the time series of voxel activities combine to provide information about internal and external experience? Here we seek models of fMRI decoding which are balanced between the simplicity of their interpretation and the effectiveness of their prediction. We use signals from a subject immersed in virtual reality to compare global and local methods of prediction applying both linear and nonlinear techniques of dimensionality reduction. We find that the prediction of complex stimuli is remarkably low-dimensional, saturating with less than 100 features. In particular, we build effective models based on the decorrelated components of cognitive activity in the classically-defined Brodmann areas. For some of the stimuli, the top predictive areas were surprisingly transparent, including Wernicke's area for verbal instructions, visual cortex for facial and body features, and visual-temporal regions for velocity. Direct sensory experience resulted in the most robust predictions, with the highest correlation ($c \sim 0.8$) between the predicted and experienced time series of verbal instructions. Techniques based on non-linear dimensionality reduction (Laplacian eigenmaps) performed similarly. The interpretability and relative simplicity of our approach provides a conceptual basis upon which to build more sophisticated techniques for fMRI decoding and offers a window into cognitive function during dynamic, natural experience.