Probability density estimation for sets of large graphs with respect to spectral information using stochastic block models

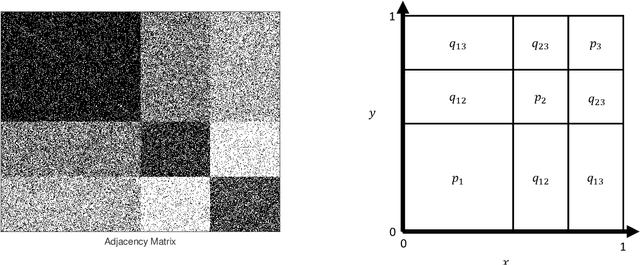
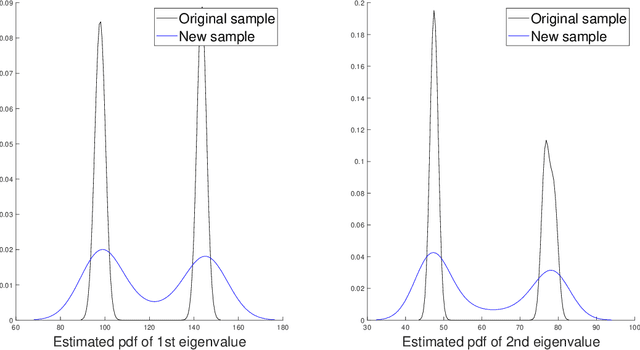
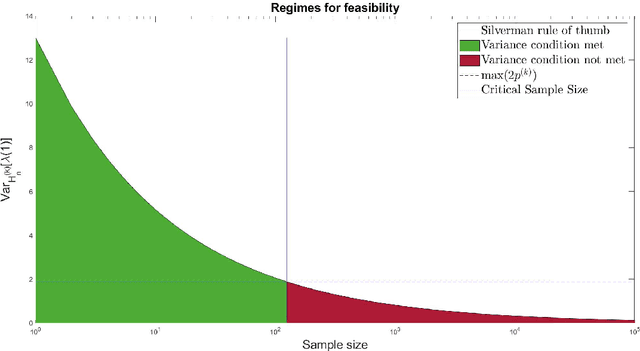
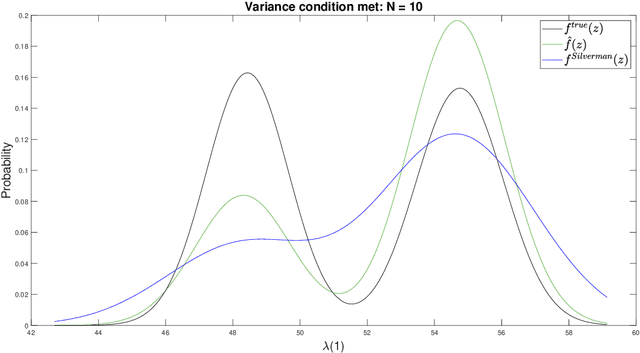
For graph-valued data sampled iid from a distribution $\mu$, the sample moments are computed with respect to a choice of metric. In this work, we equip the set of graphs with the pseudo-metric defined by the $\ell_2$ norm between the eigenvalues of the respective adjacency matrices. We use this pseudo metric and the respective sample moments of a graph valued data set to infer the parameters of a distribution $\hat{\mu}$ and interpret this distribution as an approximation of $\mu$. We verify experimentally that complex distributions $\mu$ can be approximated well taking this approach.

Theoretical analysis and computation of the sample Frechet mean for sets of large graphs based on spectral information

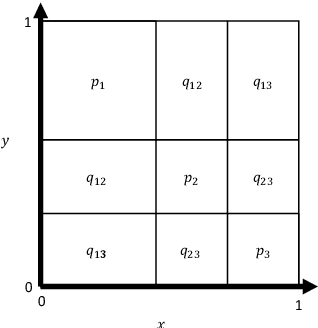
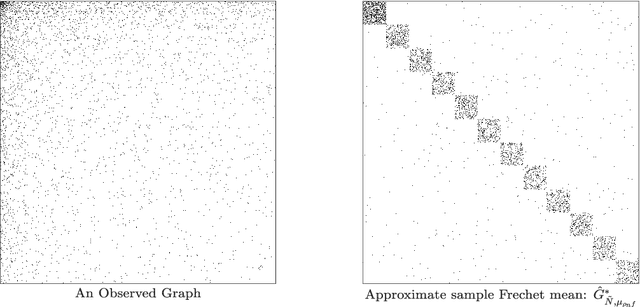
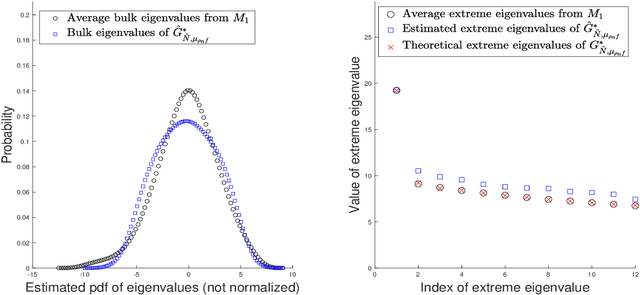
To characterize the location (mean, median) of a set of graphs, one needs a notion of centrality that is adapted to metric spaces, since graph sets are not Euclidean spaces. A standard approach is to consider the Frechet mean. In this work, we equip a set of graphs with the pseudometric defined by the norm between the eigenvalues of their respective adjacency matrix. Unlike the edit distance, this pseudometric reveals structural changes at multiple scales, and is well adapted to studying various statistical problems for graph-valued data. We describe an algorithm to compute an approximation to the sample Frechet mean of a set of undirected unweighted graphs with a fixed size using this pseudometric.

The Sample Fréchet Mean of Sparse Graphs is Sparse

The availability of large datasets composed of graphs creates an unprecedented need to invent novel tools in statistical learning for "graph-valued random variables". To characterize the "average" of a sample of graphs, one can compute the sample Fr\'echet mean. Because the sample mean should provide an interpretable summary of the graph sample, one would expect that the structural properties of the sample be transmitted to the Fr\'echet mean. In this paper, we address the following foundational question: does the sample Fr\'echet mean inherit the structural properties of the graphs in the sample? Specifically, we prove the following result: the sample Fr\'echet mean of a set of sparse graphs is sparse. We prove the result for the graph Hamming distance, and the spectral adjacency pseudometric, using very different arguments. In fact, we prove a stronger result: the edge density of the sample Fr\'echet mean is bounded by the edge density of the graphs in the sample. This result guarantees that sparsity is an hereditary property, which can be transmitted from a graph sample to its sample Fr\'echet mean, irrespective of the method used to estimate the sample Fr\'echet mean.

Approximate Fréchet Mean for Data Sets of Sparse Graphs

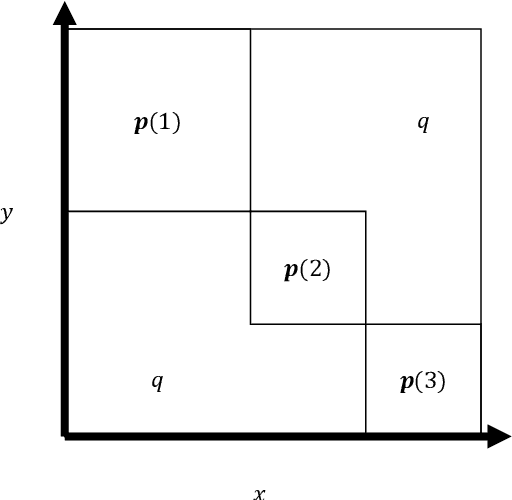
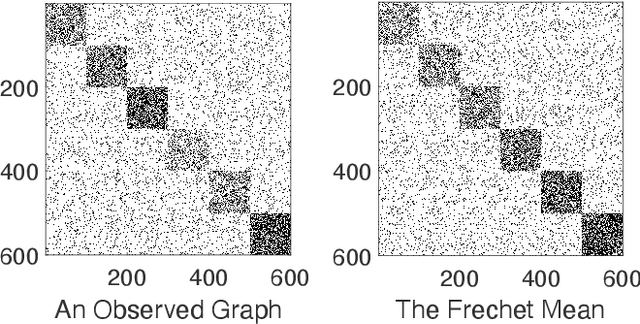
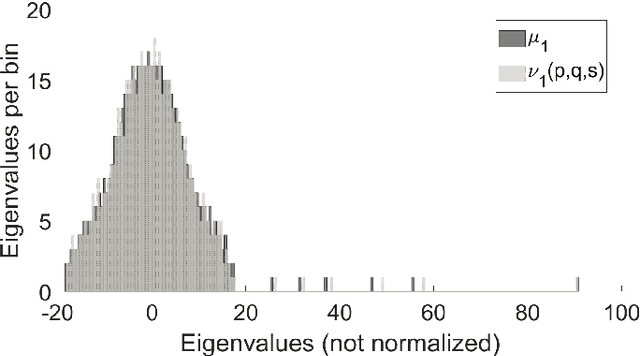
To characterize the location (mean, median) of a set of graphs, one needs a notion of centrality that is adapted to metric spaces, since graph sets are not Euclidean spaces. A standard approach is to consider the Fr\'echet mean. In this work, we equip a set of graph with the pseudometric defined by the $\ell_2$ norm between the eigenvalues of their respective adjacency matrix . Unlike the edit distance, this pseudometric reveals structural changes at multiple scales, and is well adapted to studying various statistical problems on sets of graphs. We describe an algorithm to compute an approximation to the Fr\'echet mean of a set of undirected unweighted graphs with a fixed size.