Probability density estimation for sets of large graphs with respect to spectral information using stochastic block models
Paper and Code
Jul 05, 2022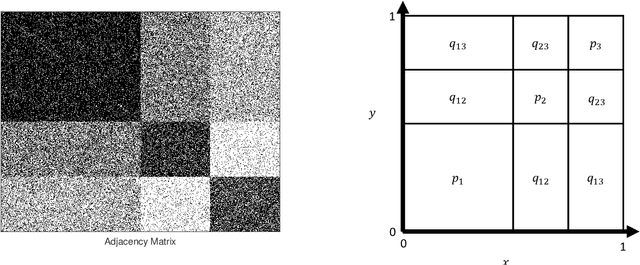
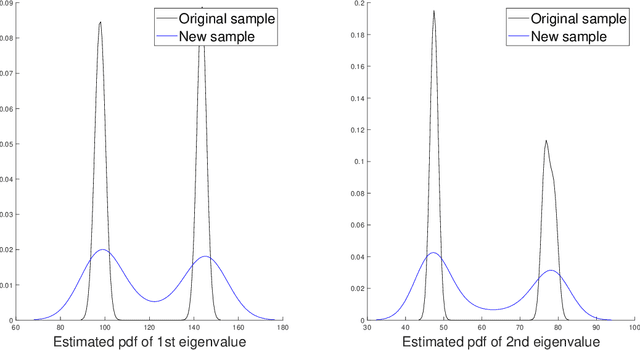
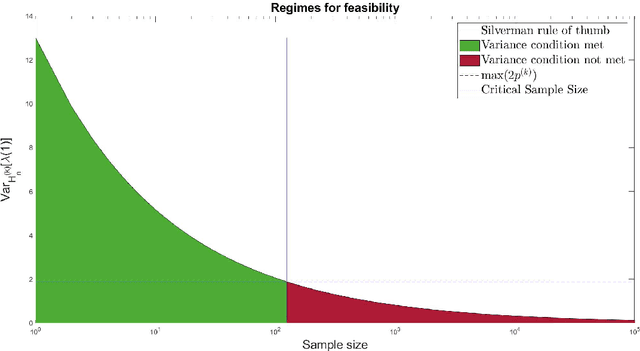
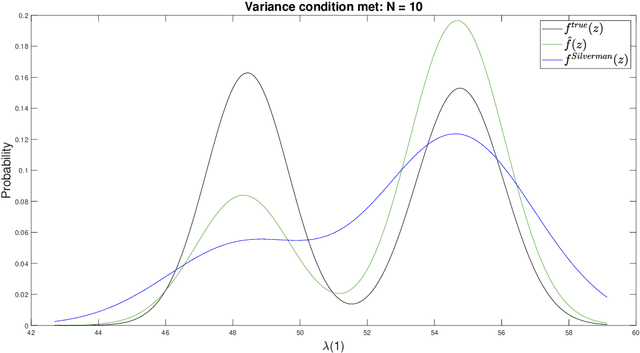
For graph-valued data sampled iid from a distribution $\mu$, the sample moments are computed with respect to a choice of metric. In this work, we equip the set of graphs with the pseudo-metric defined by the $\ell_2$ norm between the eigenvalues of the respective adjacency matrices. We use this pseudo metric and the respective sample moments of a graph valued data set to infer the parameters of a distribution $\hat{\mu}$ and interpret this distribution as an approximation of $\mu$. We verify experimentally that complex distributions $\mu$ can be approximated well taking this approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge