Estimation of the Sample Frechet Mean: A Convolutional Neural Network Approach

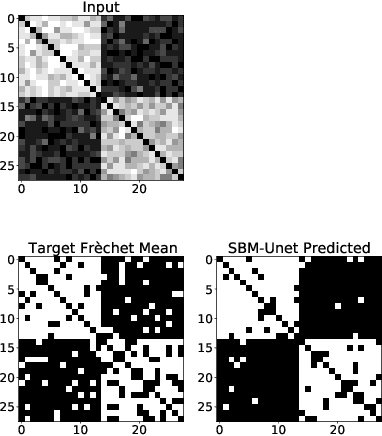
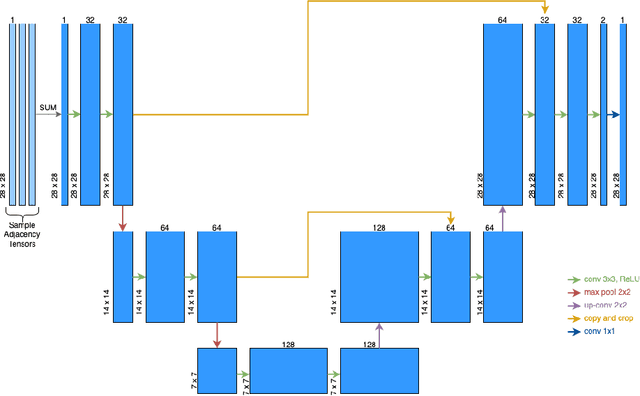
This work addresses the rising demand for novel tools in statistical and machine learning for "graph-valued random variables" by proposing a fast algorithm to compute the sample Frechet mean, which replaces the concept of sample mean for graphs (or networks). We use convolutional neural networks to learn the morphology of the graphs in a set of graphs. Our experiments on several ensembles of random graphs demonstrate that our method can reliably recover the sample Frechet mean.

Probability density estimation for sets of large graphs with respect to spectral information using stochastic block models

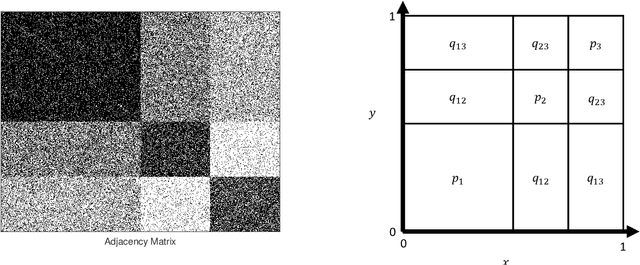
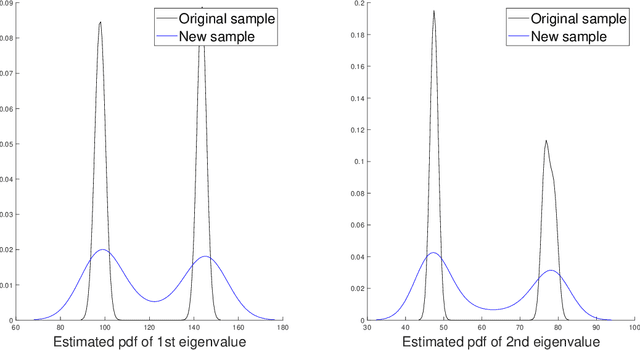
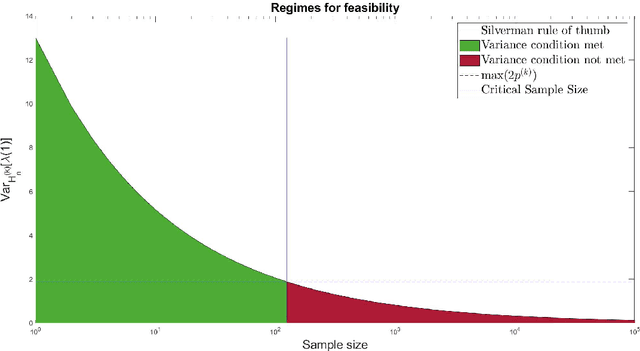
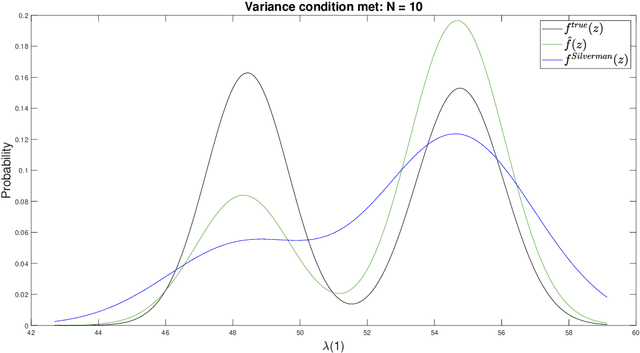
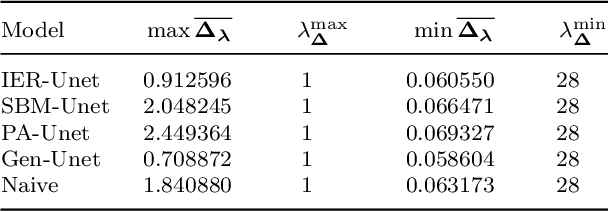
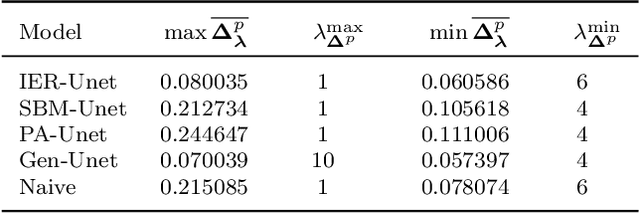
For graph-valued data sampled iid from a distribution $\mu$, the sample moments are computed with respect to a choice of metric. In this work, we equip the set of graphs with the pseudo-metric defined by the $\ell_2$ norm between the eigenvalues of the respective adjacency matrices. We use this pseudo metric and the respective sample moments of a graph valued data set to infer the parameters of a distribution $\hat{\mu}$ and interpret this distribution as an approximation of $\mu$. We verify experimentally that complex distributions $\mu$ can be approximated well taking this approach.

Approximate Fréchet Mean for Data Sets of Sparse Graphs

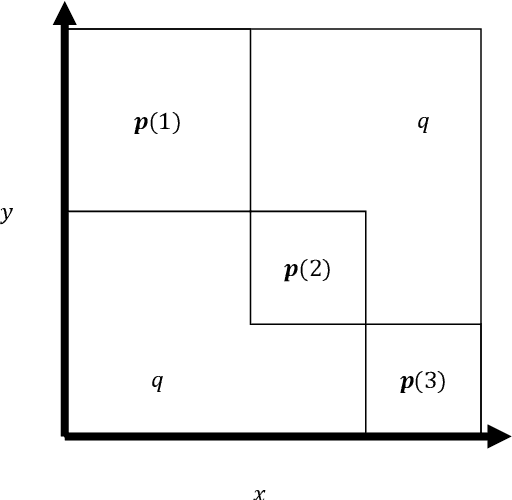
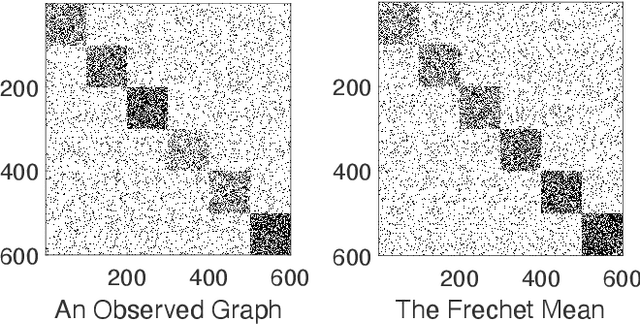
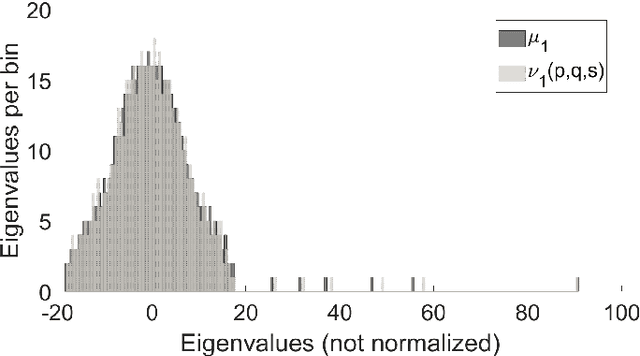
To characterize the location (mean, median) of a set of graphs, one needs a notion of centrality that is adapted to metric spaces, since graph sets are not Euclidean spaces. A standard approach is to consider the Fr\'echet mean. In this work, we equip a set of graph with the pseudometric defined by the $\ell_2$ norm between the eigenvalues of their respective adjacency matrix . Unlike the edit distance, this pseudometric reveals structural changes at multiple scales, and is well adapted to studying various statistical problems on sets of graphs. We describe an algorithm to compute an approximation to the Fr\'echet mean of a set of undirected unweighted graphs with a fixed size.

Decoding Epileptogenesis in a Reduced State Space

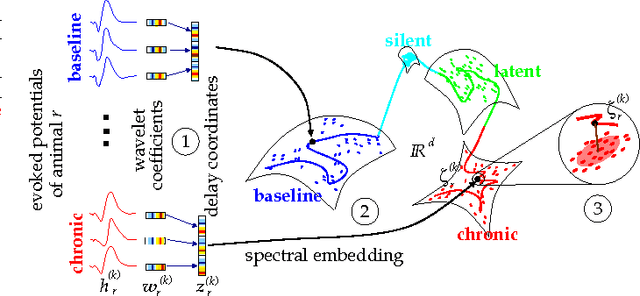
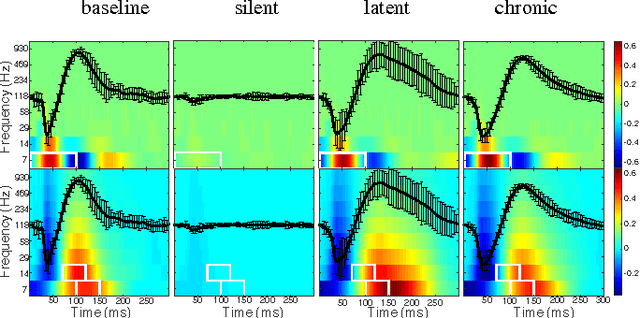
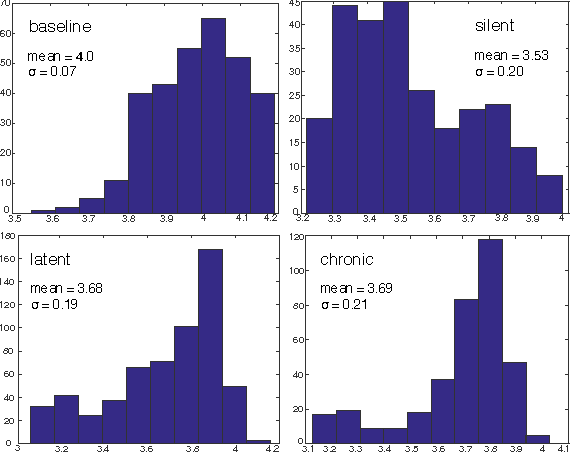
We describe here the recent results of a multidisciplinary effort to design a biomarker that can actively and continuously decode the progressive changes in neuronal organization leading to epilepsy, a process known as epileptogenesis. Using an animal model of acquired epilepsy, wechronically record hippocampal evoked potentials elicited by an auditory stimulus. Using a set of reduced coordinates, our algorithm can identify universal smooth low-dimensional configurations of the auditory evoked potentials that correspond to distinct stages of epileptogenesis. We use a hidden Markov model to learn the dynamics of the evoked potential, as it evolves along these smooth low-dimensional subsets. We provide experimental evidence that the biomarker is able to exploit subtle changes in the evoked potential to reliably decode the stage of epileptogenesis and predict whether an animal will eventually recover from the injury, or develop spontaneous seizures.

Low Dimensional Embedding of fMRI datasets

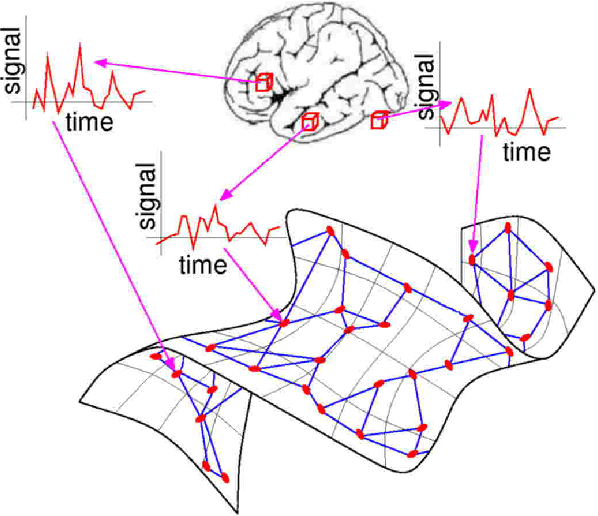
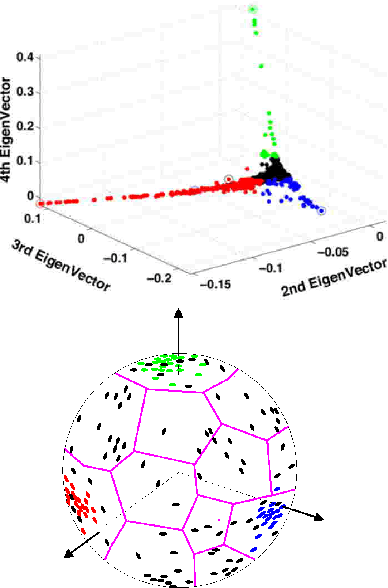
We propose a novel method to embed a functional magnetic resonance imaging (fMRI) dataset in a low-dimensional space. The embedding optimally preserves the local functional coupling between fMRI time series and provides a low-dimensional coordinate system for detecting activated voxels. To compute the embedding, we build a graph of functionally connected voxels. We use the commute time, instead of the geodesic distance, to measure functional distances on the graph. Because the commute time can be computed directly from the eigenvectors of (a symmetric version) the graph probability transition matrix, we use these eigenvectors to embed the dataset in low dimensions. After clustering the datasets in low dimensions, coherent structures emerge that can be easily interpreted. We performed an extensive evaluation of our method comparing it to linear and nonlinear techniques using synthetic datasets and in vivo datasets. We analyzed datasets from the EBC competition obtained with subjects interacting in an urban virtual reality environment. Our exploratory approach is able to detect independently visual areas (V1/V2, V5/MT), auditory areas, and language areas. Our method can be used to analyze fMRI collected during ``natural stimuli''.