Approximate Fréchet Mean for Data Sets of Sparse Graphs
Paper and Code
May 30, 2021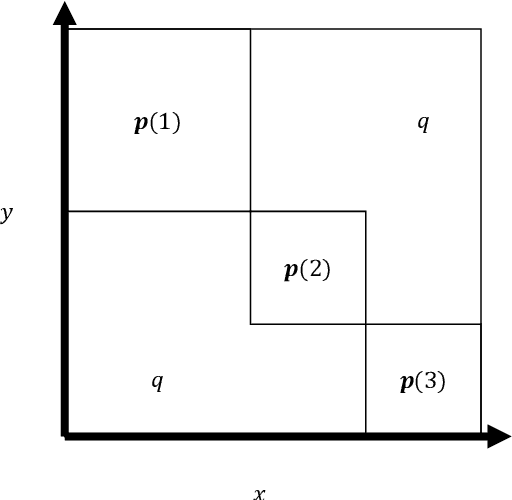

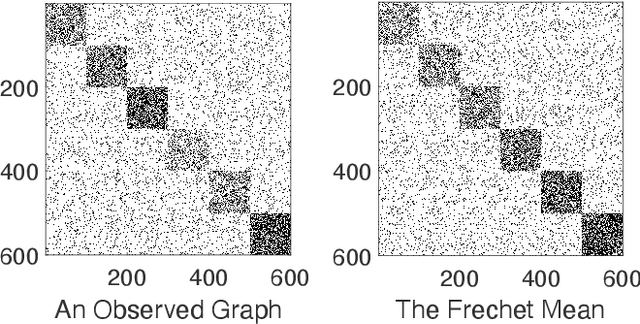
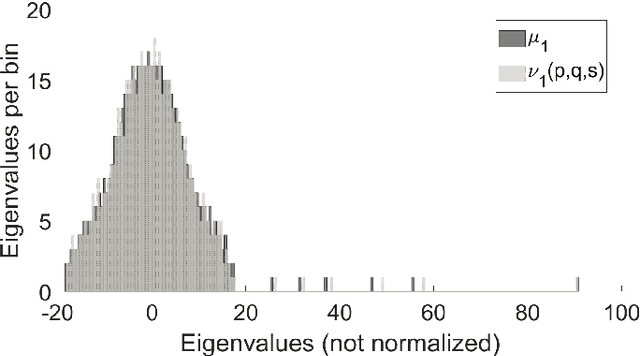
To characterize the location (mean, median) of a set of graphs, one needs a notion of centrality that is adapted to metric spaces, since graph sets are not Euclidean spaces. A standard approach is to consider the Fr\'echet mean. In this work, we equip a set of graph with the pseudometric defined by the $\ell_2$ norm between the eigenvalues of their respective adjacency matrix . Unlike the edit distance, this pseudometric reveals structural changes at multiple scales, and is well adapted to studying various statistical problems on sets of graphs. We describe an algorithm to compute an approximation to the Fr\'echet mean of a set of undirected unweighted graphs with a fixed size.
* 28 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge