Perturbation of the Eigenvectors of the Graph Laplacian: Application to Image Denoising

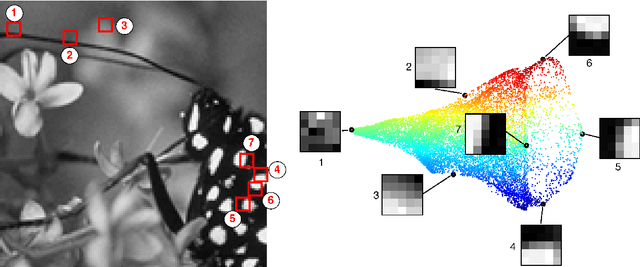
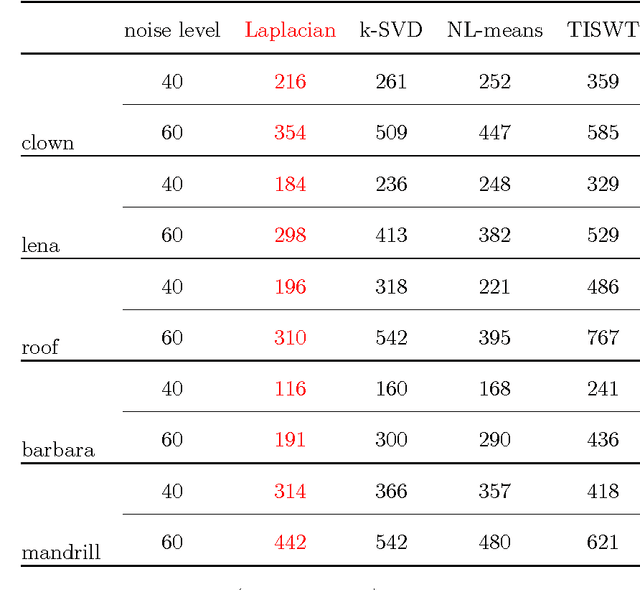
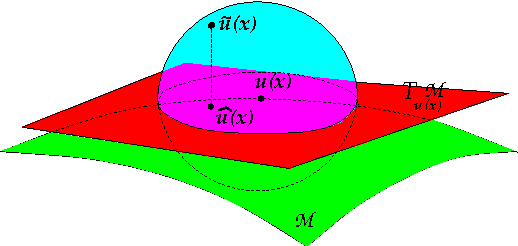
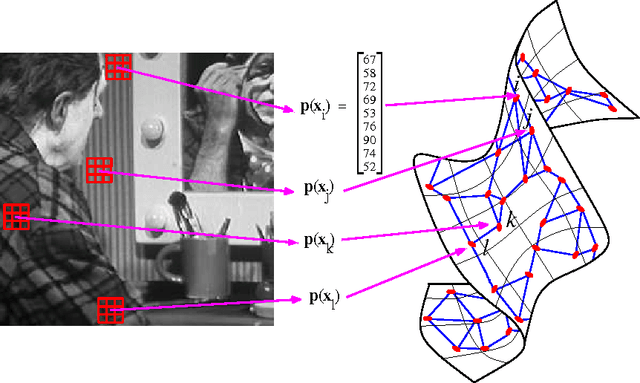
The original contributions of this paper are twofold: a new understanding of the influence of noise on the eigenvectors of the graph Laplacian of a set of image patches, and an algorithm to estimate a denoised set of patches from a noisy image. The algorithm relies on the following two observations: (1) the low-index eigenvectors of the diffusion, or graph Laplacian, operators are very robust to random perturbations of the weights and random changes in the connections of the patch-graph; and (2) patches extracted from smooth regions of the image are organized along smooth low-dimensional structures in the patch-set, and therefore can be reconstructed with few eigenvectors. Experiments demonstrate that our denoising algorithm outperforms the denoising gold-standards.

Low Dimensional Embedding of fMRI datasets

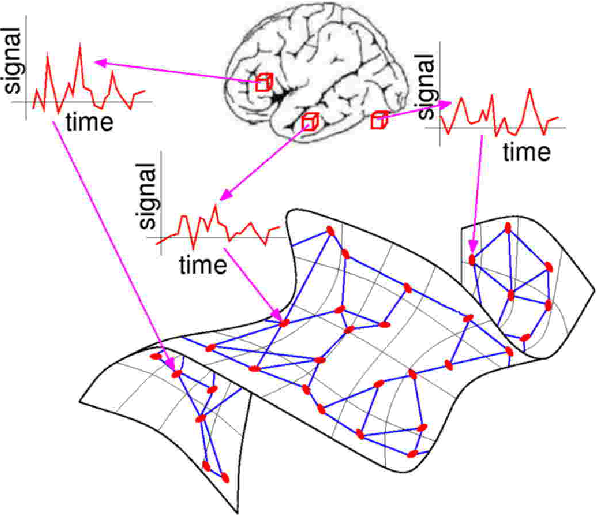
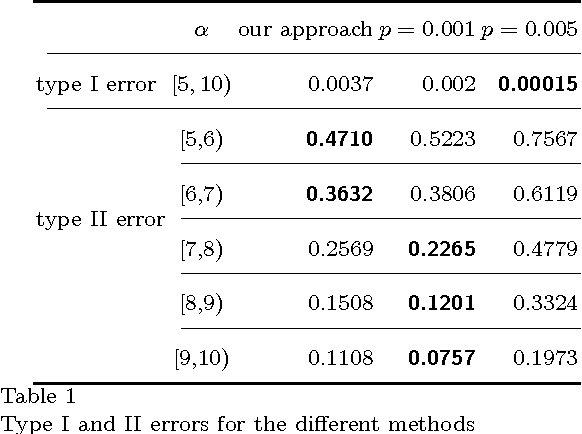
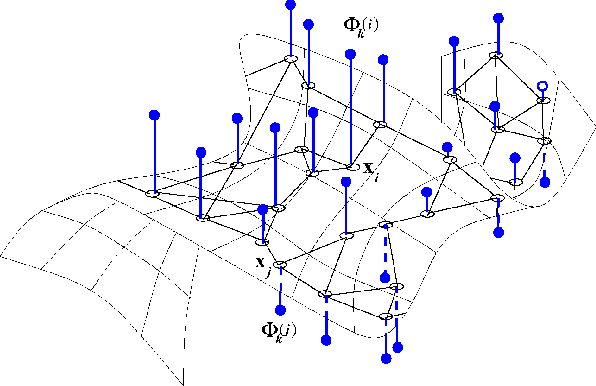
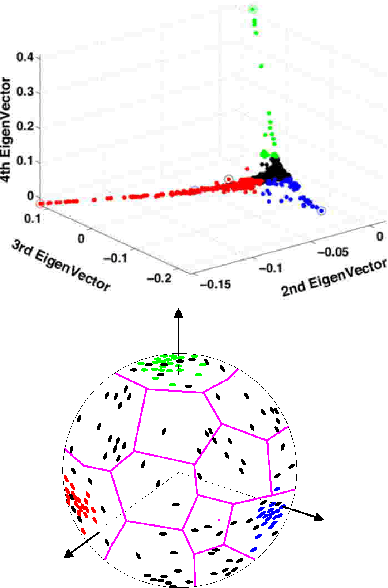
We propose a novel method to embed a functional magnetic resonance imaging (fMRI) dataset in a low-dimensional space. The embedding optimally preserves the local functional coupling between fMRI time series and provides a low-dimensional coordinate system for detecting activated voxels. To compute the embedding, we build a graph of functionally connected voxels. We use the commute time, instead of the geodesic distance, to measure functional distances on the graph. Because the commute time can be computed directly from the eigenvectors of (a symmetric version) the graph probability transition matrix, we use these eigenvectors to embed the dataset in low dimensions. After clustering the datasets in low dimensions, coherent structures emerge that can be easily interpreted. We performed an extensive evaluation of our method comparing it to linear and nonlinear techniques using synthetic datasets and in vivo datasets. We analyzed datasets from the EBC competition obtained with subjects interacting in an urban virtual reality environment. Our exploratory approach is able to detect independently visual areas (V1/V2, V5/MT), auditory areas, and language areas. Our method can be used to analyze fMRI collected during ``natural stimuli''.