Perturbation of the Eigenvectors of the Graph Laplacian: Application to Image Denoising
Paper and Code
Feb 29, 2012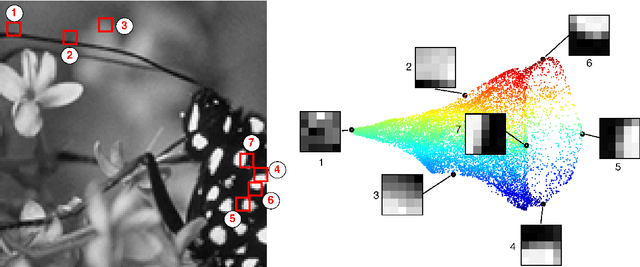
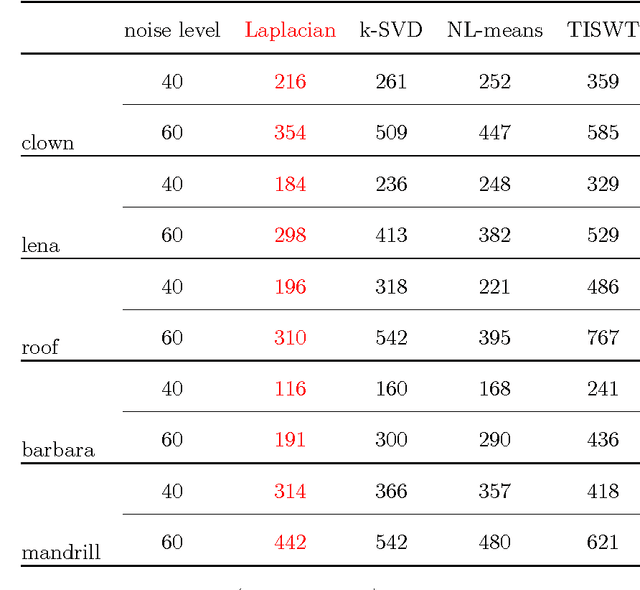
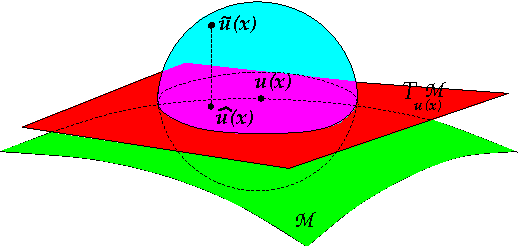
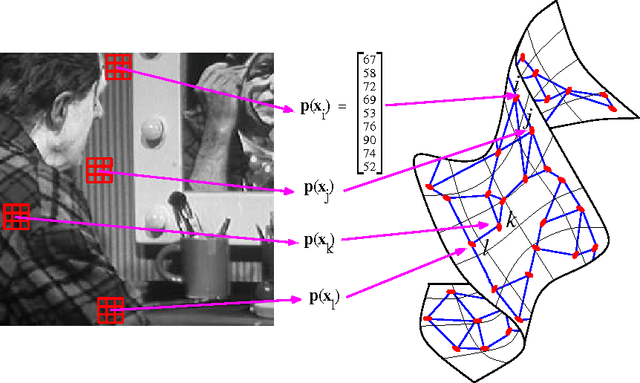
The original contributions of this paper are twofold: a new understanding of the influence of noise on the eigenvectors of the graph Laplacian of a set of image patches, and an algorithm to estimate a denoised set of patches from a noisy image. The algorithm relies on the following two observations: (1) the low-index eigenvectors of the diffusion, or graph Laplacian, operators are very robust to random perturbations of the weights and random changes in the connections of the patch-graph; and (2) patches extracted from smooth regions of the image are organized along smooth low-dimensional structures in the patch-set, and therefore can be reconstructed with few eigenvectors. Experiments demonstrate that our denoising algorithm outperforms the denoising gold-standards.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge