Inverting Nonlinear Dimensionality Reduction with Scale-Free Radial Basis Function Interpolation
Paper and Code
Nov 05, 2013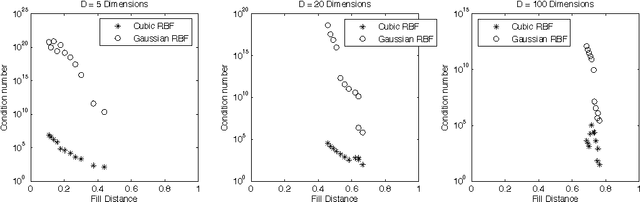
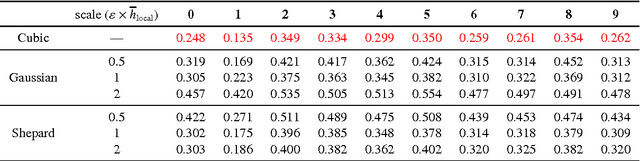
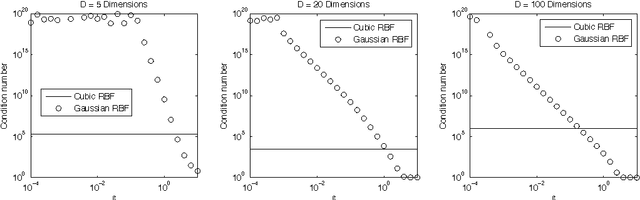

Nonlinear dimensionality reduction embeddings computed from datasets do not provide a mechanism to compute the inverse map. In this paper, we address the problem of computing a stable inverse map to such a general bi-Lipschitz map. Our approach relies on radial basis functions (RBFs) to interpolate the inverse map everywhere on the low-dimensional image of the forward map. We demonstrate that the scale-free cubic RBF kernel performs better than the Gaussian kernel: it does not suffer from ill-conditioning, and does not require the choice of a scale. The proposed construction is shown to be similar to the Nystr\"om extension of the eigenvectors of the symmetric normalized graph Laplacian matrix. Based on this observation, we provide a new interpretation of the Nystr\"om extension with suggestions for improvement.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge