Nonnegative Matrix Factorization applied to reordered pixels of single images based on patches to achieve structured nonnegative dictionaries

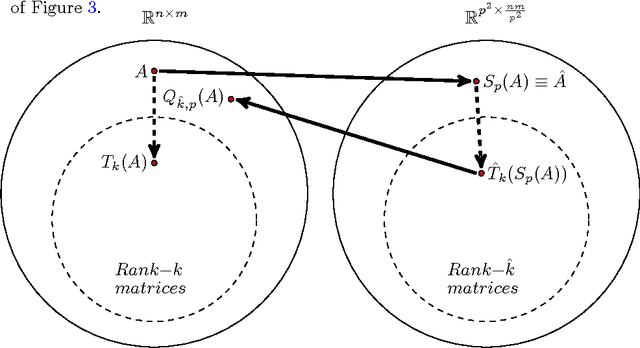
Recent improvements in computing allow for the processing and analysis of very large datasets in a variety of fields. Often the analysis requires the creation of low-rank approximations to the datasets leading to efficient storage. This article presents and analyzes a novel approach for creating nonnegative, structured dictionaries using NMF applied to reordered pixels of single, natural images. We reorder the pixels based on patches and present our approach in general. We investigate our approach when using the Singular Value Decomposition (SVD) and Nonnegative Matrix Factorizations (NMF) as low-rank approximations. Peak Signal-to-Noise Ratio (PSNR) and Mean Structural Similarity Index (MSSIM) are used to evaluate the algorithm. We report that while the SVD provides the best reconstructions, its dictionary of vectors lose both the sign structure of the original image and details of localized image content. In contrast, the dictionaries produced using NMF preserves the sign structure of the original image matrix and offer a nonnegative, parts-based dictionary.

A random walk on image patches

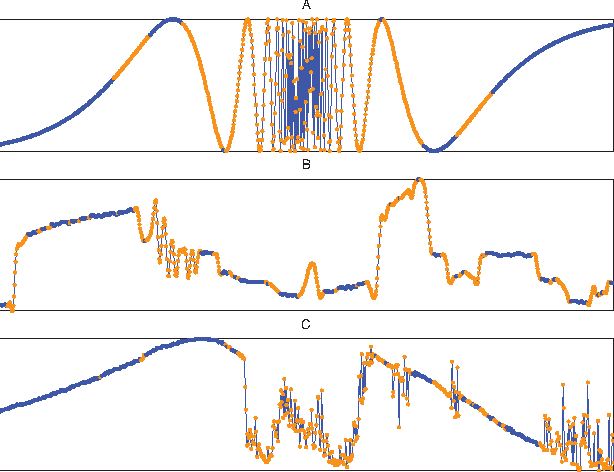
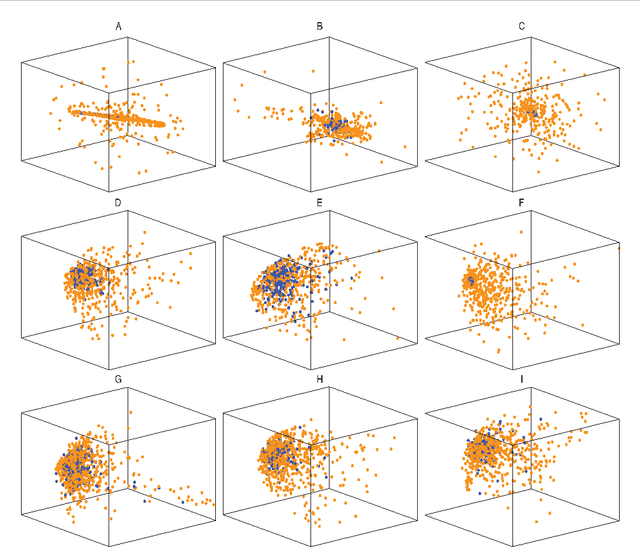
In this paper we address the problem of understanding the success of algorithms that organize patches according to graph-based metrics. Algorithms that analyze patches extracted from images or time series have led to state-of-the art techniques for classification, denoising, and the study of nonlinear dynamics. The main contribution of this work is to provide a theoretical explanation for the above experimental observations. Our approach relies on a detailed analysis of the commute time metric on prototypical graph models that epitomize the geometry observed in general patch graphs. We prove that a parametrization of the graph based on commute times shrinks the mutual distances between patches that correspond to rapid local changes in the signal, while the distances between patches that correspond to slow local changes expand. In effect, our results explain why the parametrization of the set of patches based on the eigenfunctions of the Laplacian can concentrate patches that correspond to rapid local changes, which would otherwise be shattered in the space of patches. While our results are based on a large sample analysis, numerical experimentations on synthetic and real data indicate that the results hold for datasets that are very small in practice.