A random walk on image patches
Paper and Code
Jul 02, 2011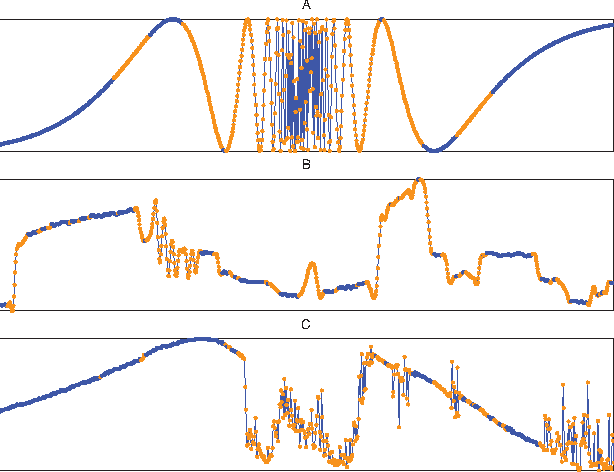


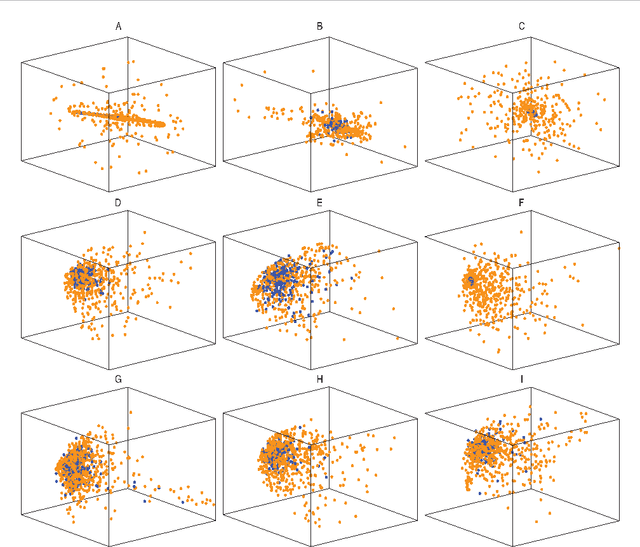
In this paper we address the problem of understanding the success of algorithms that organize patches according to graph-based metrics. Algorithms that analyze patches extracted from images or time series have led to state-of-the art techniques for classification, denoising, and the study of nonlinear dynamics. The main contribution of this work is to provide a theoretical explanation for the above experimental observations. Our approach relies on a detailed analysis of the commute time metric on prototypical graph models that epitomize the geometry observed in general patch graphs. We prove that a parametrization of the graph based on commute times shrinks the mutual distances between patches that correspond to rapid local changes in the signal, while the distances between patches that correspond to slow local changes expand. In effect, our results explain why the parametrization of the set of patches based on the eigenfunctions of the Laplacian can concentrate patches that correspond to rapid local changes, which would otherwise be shattered in the space of patches. While our results are based on a large sample analysis, numerical experimentations on synthetic and real data indicate that the results hold for datasets that are very small in practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge