Better Decisions through the Right Causal World Model

Reinforcement learning (RL) agents have shown remarkable performances in various environments, where they can discover effective policies directly from sensory inputs. However, these agents often exploit spurious correlations in the training data, resulting in brittle behaviours that fail to generalize to new or slightly modified environments. To address this, we introduce the Causal Object-centric Model Extraction Tool (COMET), a novel algorithm designed to learn the exact interpretable causal world models (CWMs). COMET first extracts object-centric state descriptions from observations and identifies the environment's internal states related to the depicted objects' properties. Using symbolic regression, it models object-centric transitions and derives causal relationships governing object dynamics. COMET further incorporates large language models (LLMs) for semantic inference, annotating causal variables to enhance interpretability. By leveraging these capabilities, COMET constructs CWMs that align with the true causal structure of the environment, enabling agents to focus on task-relevant features. The extracted CWMs mitigate the danger of shortcuts, permitting the development of RL systems capable of better planning and decision-making across dynamic scenarios. Our results, validated in Atari environments such as Pong and Freeway, demonstrate the accuracy and robustness of COMET, highlighting its potential to bridge the gap between object-centric reasoning and causal inference in reinforcement learning.

Scaling Probabilistic Circuits via Data Partitioning

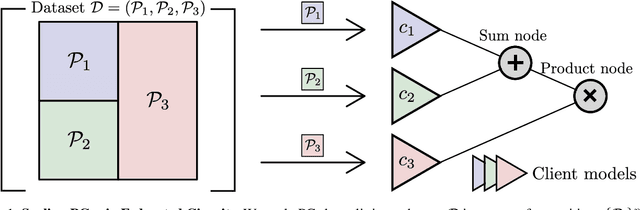
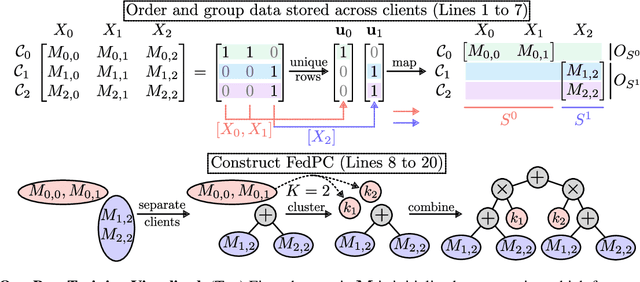
Probabilistic circuits (PCs) enable us to learn joint distributions over a set of random variables and to perform various probabilistic queries in a tractable fashion. Though the tractability property allows PCs to scale beyond non-tractable models such as Bayesian Networks, scaling training and inference of PCs to larger, real-world datasets remains challenging. To remedy the situation, we show how PCs can be learned across multiple machines by recursively partitioning a distributed dataset, thereby unveiling a deep connection between PCs and federated learning (FL). This leads to federated circuits (FCs) -- a novel and flexible federated learning (FL) framework that (1) allows one to scale PCs on distributed learning environments (2) train PCs faster and (3) unifies for the first time horizontal, vertical, and hybrid FL in one framework by re-framing FL as a density estimation problem over distributed datasets. We demonstrate FC's capability to scale PCs on various large-scale datasets. Also, we show FC's versatility in handling horizontal, vertical, and hybrid FL within a unified framework on multiple classification tasks.

Systems with Switching Causal Relations: A Meta-Causal Perspective

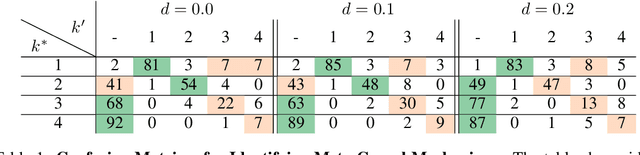
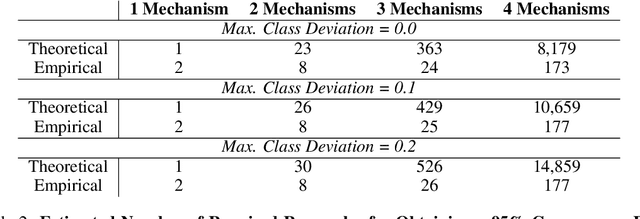
Most work on causality in machine learning assumes that causal relationships are driven by a constant underlying process. However, the flexibility of agents' actions or tipping points in the environmental process can change the qualitative dynamics of the system. As a result, new causal relationships may emerge, while existing ones change or disappear, resulting in an altered causal graph. To analyze these qualitative changes on the causal graph, we propose the concept of meta-causal states, which groups classical causal models into clusters based on equivalent qualitative behavior and consolidates specific mechanism parameterizations. We demonstrate how meta-causal states can be inferred from observed agent behavior, and discuss potential methods for disentangling these states from unlabeled data. Finally, we direct our analysis towards the application of a dynamical system, showing that meta-causal states can also emerge from inherent system dynamics, and thus constitute more than a context-dependent framework in which mechanisms emerge only as a result of external factors.

Where is the Truth? The Risk of Getting Confounded in a Continual World

A dataset is confounded if it is most easily solved via a spurious correlation which fails to generalize to new data. We will show that, in a continual learning setting where confounders may vary in time across tasks, the resulting challenge far exceeds the standard forgetting problem normally considered. In particular, we derive mathematically the effect of such confounders on the space of valid joint solutions to sets of confounded tasks. Interestingly, our theory predicts that for many such continual datasets, spurious correlations are easily ignored when the tasks are trained on jointly, but it is far harder to avoid confounding when they are considered sequentially. We construct such a dataset and demonstrate empirically that standard continual learning methods fail to ignore confounders, while training jointly on all tasks is successful. Our continually confounded dataset, ConCon, is based on CLEVR images and demonstrates the need for continual learning methods with more robust behavior with respect to confounding.

Continual Causal Abstractions

This short paper discusses continually updated causal abstractions as a potential direction of future research. The key idea is to revise the existing level of causal abstraction to a different level of detail that is both consistent with the history of observed data and more effective in solving a given task.

Attributions Beyond Neural Networks: The Linear Program Case

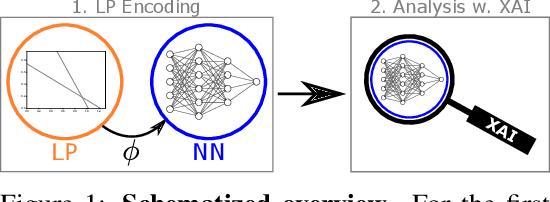
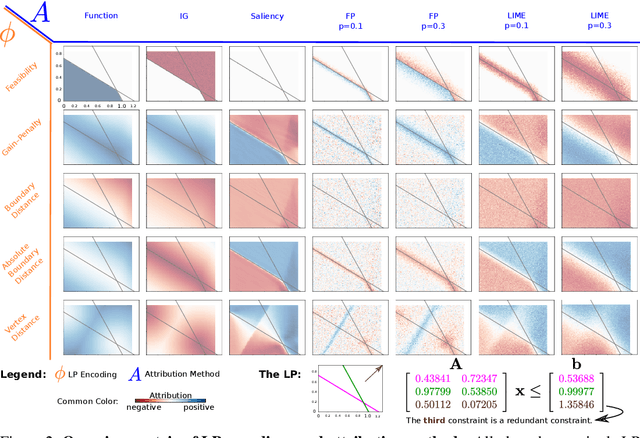
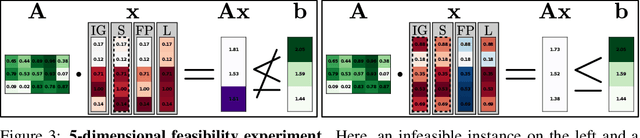
Linear Programs (LPs) have been one of the building blocks in machine learning and have championed recent strides in differentiable optimizers for learning systems. While there exist solvers for even high-dimensional LPs, understanding said high-dimensional solutions poses an orthogonal and unresolved problem. We introduce an approach where we consider neural encodings for LPs that justify the application of attribution methods from explainable artificial intelligence (XAI) designed for neural learning systems. The several encoding functions we propose take into account aspects such as feasibility of the decision space, the cost attached to each input, or the distance to special points of interest. We investigate the mathematical consequences of several XAI methods on said neural LP encodings. We empirically show that the attribution methods Saliency and LIME reveal indistinguishable results up to perturbation levels, and we propose the property of Directedness as the main discriminative criterion between Saliency and LIME on one hand, and a perturbation-based Feature Permutation approach on the other hand. Directedness indicates whether an attribution method gives feature attributions with respect to an increase of that feature. We further notice the baseline selection problem beyond the classical computer vision setting for Integrated Gradients.

Finding Structure and Causality in Linear Programs

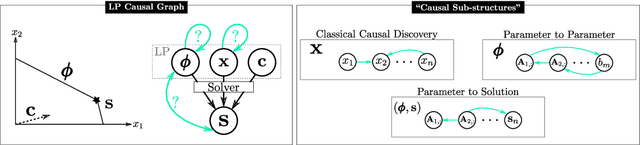
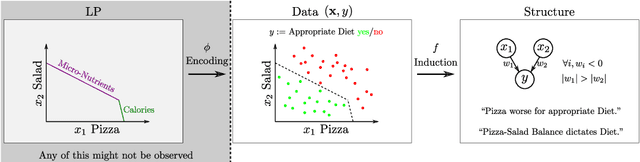
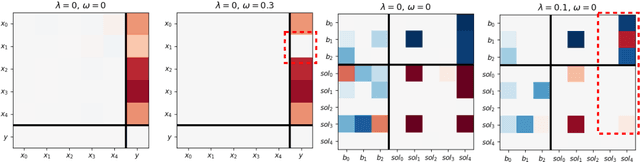
Linear Programs (LP) are celebrated widely, particularly so in machine learning where they have allowed for effectively solving probabilistic inference tasks or imposing structure on end-to-end learning systems. Their potential might seem depleted but we propose a foundational, causal perspective that reveals intriguing intra- and inter-structure relations for LP components. We conduct a systematic, empirical investigation on general-, shortest path- and energy system LPs.