Policies and Evaluation for Online Meeting Summarization

With more and more meetings moving to a digital domain, meeting summarization has recently gained interest in both academic and commercial research. However, prior academic research focuses on meeting summarization as an offline task, performed after the meeting concludes. In this paper, we perform the first systematic study of online meeting summarization. For this purpose, we propose several policies for conducting online summarization. We discuss the unique challenges of this task compared to the offline setting and define novel metrics to evaluate latency and partial summary quality. The experiments on the AutoMin dataset show that 1) online models can produce strong summaries, 2) our metrics allow a detailed analysis of different systems' quality-latency trade-off, also taking into account intermediate outputs and 3) adaptive policies perform better than fixed scheduled ones. These findings provide a starting point for the wider research community to explore this important task.

Maximum a Posteriori Estimation for Linear Structural Dynamics Models Using Bayesian Optimization with Rational Polynomial Chaos Expansions

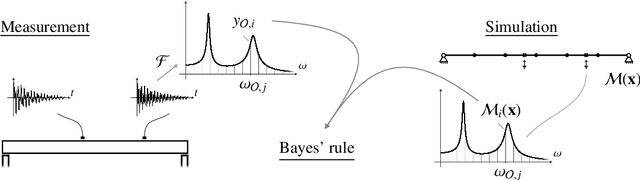
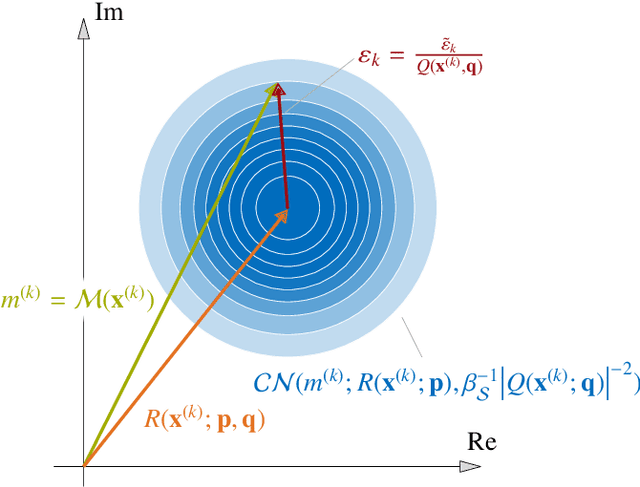
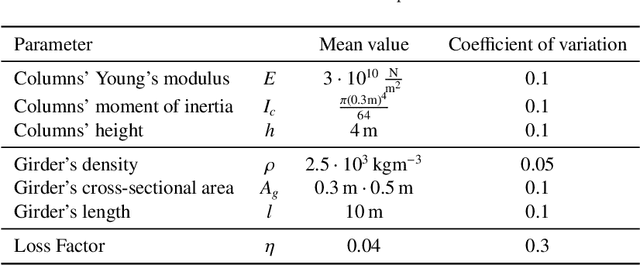
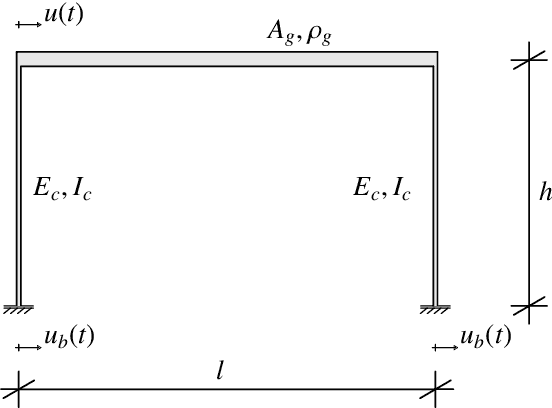
Bayesian analysis enables combining prior knowledge with measurement data to learn model parameters. Commonly, one resorts to computing the maximum a posteriori (MAP) estimate, when only a point estimate of the parameters is of interest. We apply MAP estimation in the context of structural dynamic models, where the system response can be described by the frequency response function. To alleviate high computational demands from repeated expensive model calls, we utilize a rational polynomial chaos expansion (RPCE) surrogate model that expresses the system frequency response as a rational of two polynomials with complex coefficients. We propose an extension to an existing sparse Bayesian learning approach for RPCE based on Laplace's approximation for the posterior distribution of the denominator coefficients. Furthermore, we introduce a Bayesian optimization approach, which allows to adaptively enrich the experimental design throughout the optimization process of MAP estimation. Thereby, we utilize the expected improvement acquisition function as a means to identify sample points in the input space that are possibly associated with large objective function values. The acquisition function is estimated through Monte Carlo sampling based on the posterior distribution of the expansion coefficients identified in the sparse Bayesian learning process. By combining the sparsity-inducing learning procedure with the sequential experimental design, we effectively reduce the number of model evaluations in the MAP estimation problem. We demonstrate the applicability of the presented methods on the parameter updating problem of an algebraic two-degree-of-freedom system and the finite element model of a cross-laminated timber plate.

Sparse Bayesian Learning for Complex-Valued Rational Approximations

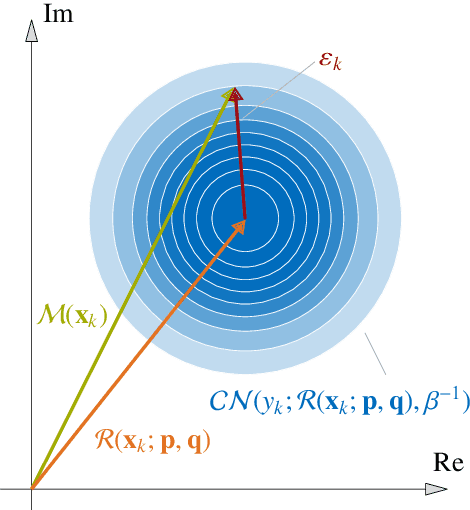
Surrogate models are used to alleviate the computational burden in engineering tasks, which require the repeated evaluation of computationally demanding models of physical systems, such as the efficient propagation of uncertainties. For models that show a strongly non-linear dependence on their input parameters, standard surrogate techniques, such as polynomial chaos expansion, are not sufficient to obtain an accurate representation of the original model response. Through applying a rational approximation instead, the approximation error can be efficiently reduced for models whose non-linearity is accurately described through a rational function. Specifically, our aim is to approximate complex-valued models. A common approach to obtain the coefficients in the surrogate is to minimize the sample-based error between model and surrogate in the least-square sense. In order to obtain an accurate representation of the original model and to avoid overfitting, the sample set has be two to three times the number of polynomial terms in the expansion. For models that require a high polynomial degree or are high-dimensional in terms of their input parameters, this number often exceeds the affordable computational cost. To overcome this issue, we apply a sparse Bayesian learning approach to the rational approximation. Through a specific prior distribution structure, sparsity is induced in the coefficients of the surrogate model. The denominator polynomial coefficients as well as the hyperparameters of the problem are determined through a type-II-maximum likelihood approach. We apply a quasi-Newton gradient-descent algorithm in order to find the optimal denominator coefficients and derive the required gradients through application of $\mathbb{CR}$-calculus.

ELITR Non-Native Speech Translation at IWSLT 2020

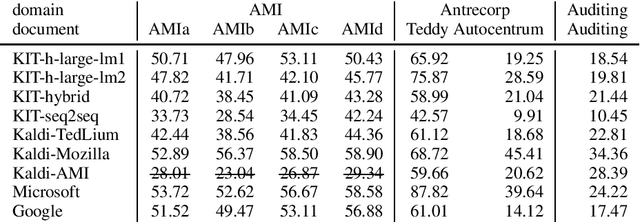
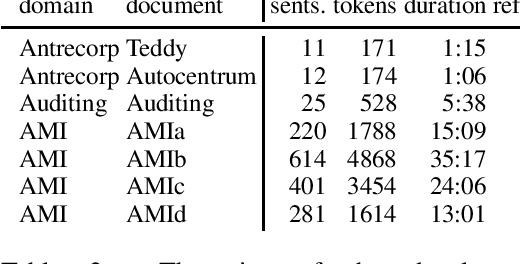
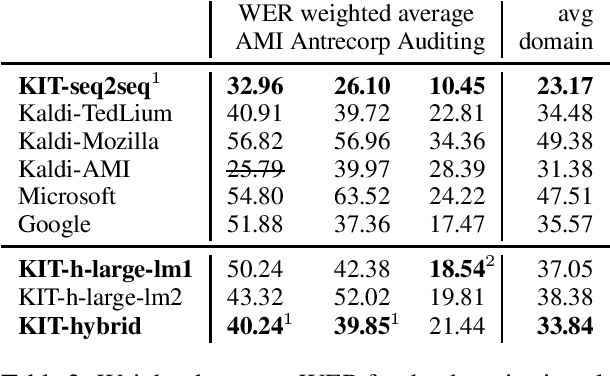
This paper is an ELITR system submission for the non-native speech translation task at IWSLT 2020. We describe systems for offline ASR, real-time ASR, and our cascaded approach to offline SLT and real-time SLT. We select our primary candidates from a pool of pre-existing systems, develop a new end-to-end general ASR system, and a hybrid ASR trained on non-native speech. The provided small validation set prevents us from carrying out a complex validation, but we submit all the unselected candidates for contrastive evaluation on the test set.