Post-training for Efficient Communication via Convention Formation

Humans communicate with increasing efficiency in multi-turn interactions, by adapting their language and forming ad-hoc conventions. In contrast, prior work shows that LLMs do not naturally show this behavior. We develop a post-training process to develop this ability through targeted fine-tuning on heuristically identified demonstrations of convention formation. We evaluate with two new benchmarks focused on this capability. First, we design a focused, cognitively-motivated interaction benchmark that consistently elicits strong convention formation trends in humans. Second, we create a new document-grounded reference completion task that reflects in-the-wild convention formation behavior. Our studies show significantly improved convention formation abilities in post-trained LLMs across the two evaluation methods.

Consistency Checks for Language Model Forecasters

Forecasting is a task that is difficult to evaluate: the ground truth can only be known in the future. Recent work showing LLM forecasters rapidly approaching human-level performance begs the question: how can we benchmark and evaluate these forecasters instantaneously? Following the consistency check framework, we measure the performance of forecasters in terms of the consistency of their predictions on different logically-related questions. We propose a new, general consistency metric based on arbitrage: for example, if a forecasting AI illogically predicts that both the Democratic and Republican parties have 60% probability of winning the 2024 US presidential election, an arbitrageur can trade against the forecaster's predictions and make a profit. We build an automated evaluation system that generates a set of base questions, instantiates consistency checks from these questions, elicits the predictions of the forecaster, and measures the consistency of the predictions. We then build a standard, proper-scoring-rule forecasting benchmark, and show that our (instantaneous) consistency metrics correlate with LLM forecasters' ground truth Brier scores (which are only known in the future). We also release a consistency benchmark that resolves in 2028, providing a long-term evaluation tool for forecasting.

Planning In Natural Language Improves LLM Search For Code Generation

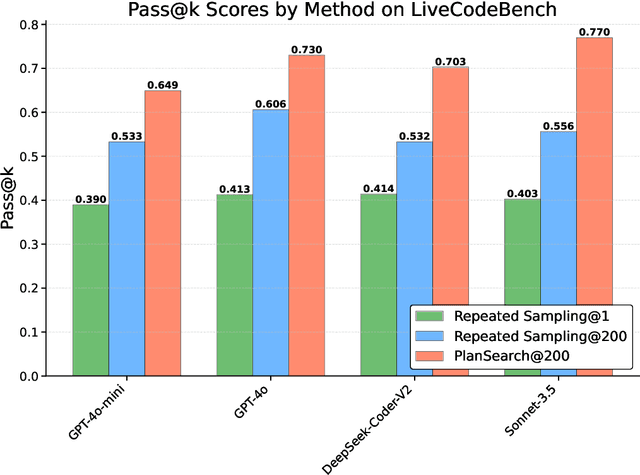
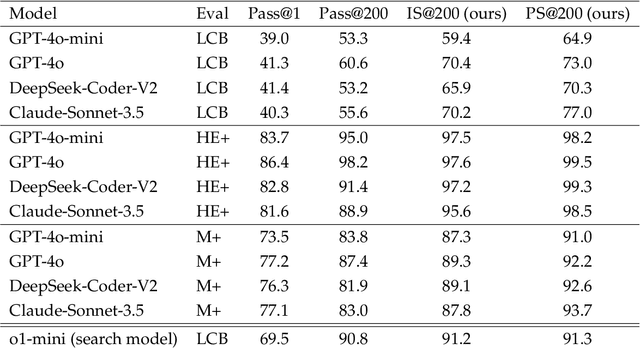
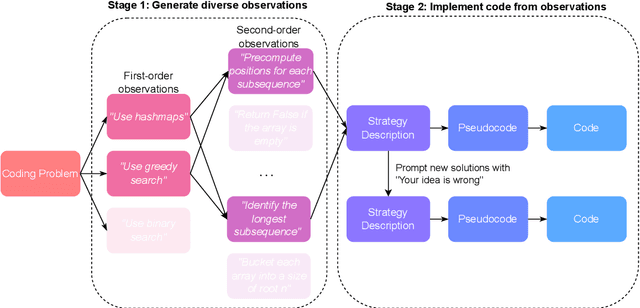
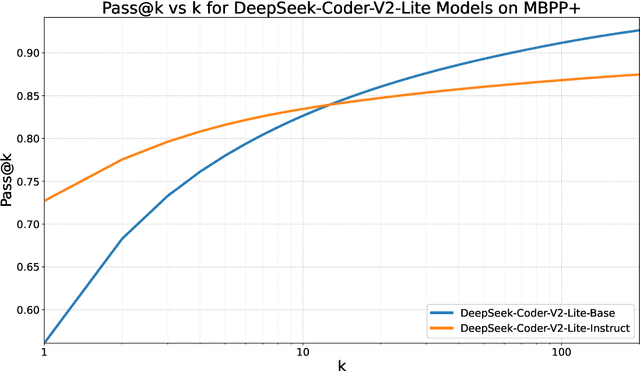
While scaling training compute has led to remarkable improvements in large language models (LLMs), scaling inference compute has not yet yielded analogous gains. We hypothesize that a core missing component is a lack of diverse LLM outputs, leading to inefficient search due to models repeatedly sampling highly similar, yet incorrect generations. We empirically demonstrate that this lack of diversity can be mitigated by searching over candidate plans for solving a problem in natural language. Based on this insight, we propose PLANSEARCH, a novel search algorithm which shows strong results across HumanEval+, MBPP+, and LiveCodeBench (a contamination-free benchmark for competitive coding). PLANSEARCH generates a diverse set of observations about the problem and then uses these observations to construct plans for solving the problem. By searching over plans in natural language rather than directly over code solutions, PLANSEARCH explores a significantly more diverse range of potential solutions compared to baseline search methods. Using PLANSEARCH on top of Claude 3.5 Sonnet achieves a state-of-the-art pass@200 of 77.0% on LiveCodeBench, outperforming both the best score achieved without search (pass@1 = 41.4%) and using standard repeated sampling (pass@200 = 60.6%). Finally, we show that, across all models, search algorithms, and benchmarks analyzed, we can accurately predict performance gains due to search as a direct function of the diversity over generated ideas.

SWIFT: Rapid Decentralized Federated Learning via Wait-Free Model Communication

The decentralized Federated Learning (FL) setting avoids the role of a potentially unreliable or untrustworthy central host by utilizing groups of clients to collaboratively train a model via localized training and model/gradient sharing. Most existing decentralized FL algorithms require synchronization of client models where the speed of synchronization depends upon the slowest client. In this work, we propose SWIFT: a novel wait-free decentralized FL algorithm that allows clients to conduct training at their own speed. Theoretically, we prove that SWIFT matches the gold-standard iteration convergence rate $\mathcal{O}(1/\sqrt{T})$ of parallel stochastic gradient descent for convex and non-convex smooth optimization (total iterations $T$). Furthermore, we provide theoretical results for IID and non-IID settings without any bounded-delay assumption for slow clients which is required by other asynchronous decentralized FL algorithms. Although SWIFT achieves the same iteration convergence rate with respect to $T$ as other state-of-the-art (SOTA) parallel stochastic algorithms, it converges faster with respect to run-time due to its wait-free structure. Our experimental results demonstrate that SWIFT's run-time is reduced due to a large reduction in communication time per epoch, which falls by an order of magnitude compared to synchronous counterparts. Furthermore, SWIFT produces loss levels for image classification, over IID and non-IID data settings, upwards of 50% faster than existing SOTA algorithms.