Uncertainty-aware retinal layer segmentation in OCT through probabilistic signed distance functions

In this paper, we present a new approach for uncertainty-aware retinal layer segmentation in Optical Coherence Tomography (OCT) scans using probabilistic signed distance functions (SDF). Traditional pixel-wise and regression-based methods primarily encounter difficulties in precise segmentation and lack of geometrical grounding respectively. To address these shortcomings, our methodology refines the segmentation by predicting a signed distance function (SDF) that effectively parameterizes the retinal layer shape via level set. We further enhance the framework by integrating probabilistic modeling, applying Gaussian distributions to encapsulate the uncertainty in the shape parameterization. This ensures a robust representation of the retinal layer morphology even in the presence of ambiguous input, imaging noise, and unreliable segmentations. Both quantitative and qualitative evaluations demonstrate superior performance when compared to other methods. Additionally, we conducted experiments on artificially distorted datasets with various noise types-shadowing, blinking, speckle, and motion-common in OCT scans to showcase the effectiveness of our uncertainty estimation. Our findings demonstrate the possibility to obtain reliable segmentation of retinal layers, as well as an initial step towards the characterization of layer integrity, a key biomarker for disease progression. Our code is available at \url{https://github.com/niazoys/RLS_PSDF}.

Grounding Continuous Representations in Geometry: Equivariant Neural Fields

Recently, Neural Fields have emerged as a powerful modelling paradigm to represent continuous signals. In a conditional neural field, a field is represented by a latent variable that conditions the NeF, whose parametrisation is otherwise shared over an entire dataset. We propose Equivariant Neural Fields based on cross attention transformers, in which NeFs are conditioned on a geometric conditioning variable, a latent point cloud, that enables an equivariant decoding from latent to field. Our equivariant approach induces a steerability property by which both field and latent are grounded in geometry and amenable to transformation laws if the field transforms, the latent represents transforms accordingly and vice versa. Crucially, the equivariance relation ensures that the latent is capable of (1) representing geometric patterns faitfhully, allowing for geometric reasoning in latent space, (2) weightsharing over spatially similar patterns, allowing for efficient learning of datasets of fields. These main properties are validated using classification experiments and a verification of the capability of fitting entire datasets, in comparison to other non-equivariant NeF approaches. We further validate the potential of ENFs by demonstrate unique local field editing properties.

Fast, Expressive SE$(n)$ Equivariant Networks through Weight-Sharing in Position-Orientation Space

Based on the theory of homogeneous spaces we derive \textit{geometrically optimal edge attributes} to be used within the flexible message passing framework. We formalize the notion of weight sharing in convolutional networks as the sharing of message functions over point-pairs that should be treated equally. We define equivalence classes of point-pairs that are identical up to a transformation in the group and derive attributes that uniquely identify these classes. Weight sharing is then obtained by conditioning message functions on these attributes. As an application of the theory, we develop an efficient equivariant group convolutional network for processing 3D point clouds. The theory of homogeneous spaces tells us how to do group convolutions with feature maps over the homogeneous space of positions $\mathbb{R}^3$, position and orientations $\mathbb{R}^3 {\times} S^2$, and the group SE$(3)$ itself. Among these, $\mathbb{R}^3 {\times} S^2$ is an optimal choice due to the ability to represent directional information, which $\mathbb{R}^3$ methods cannot, and it significantly enhances computational efficiency compared to indexing features on the full SE$(3)$ group. We empirically support this claim by reaching state-of-the-art results -- in accuracy and speed -- on three different benchmarks: interatomic potential energy prediction, trajectory forecasting in N-body systems, and generating molecules via equivariant diffusion models.

B-Spline CNNs on Lie Groups

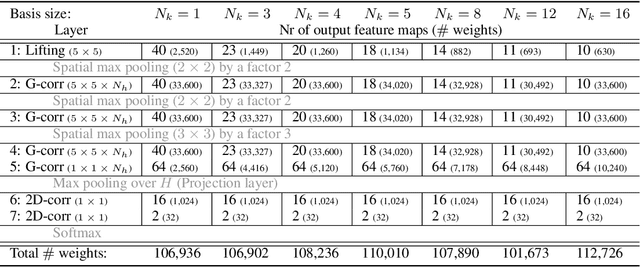
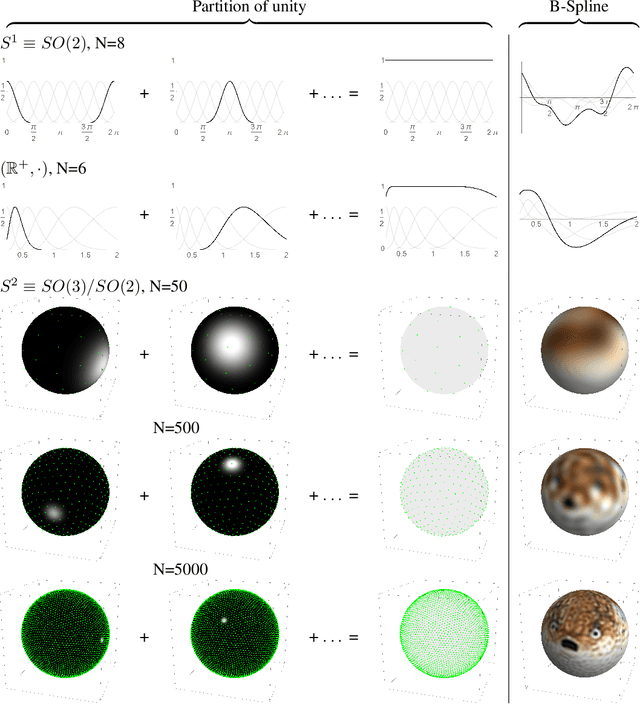
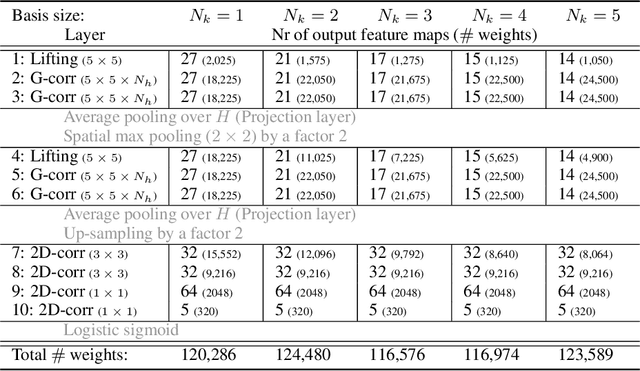
Group convolutional neural networks (G-CNNs) can be used to improve classical CNNs by equipping them with the geometric structure of groups. Central in the success of G-CNNs is the lifting of feature maps to higher dimensional disentangled representations, in which data characteristics are effectively learned, geometric data-augmentations are made obsolete, and predictable behavior under geometric transformations (equivariance) is guaranteed via group theory. Currently, however, the practical implementations of G-CNNs are limited to either discrete groups (that leave the grid intact) or continuous compact groups such as rotations (that enable the use of Fourier theory). In this paper we lift these limitations and propose a modular framework for the design and implementation of G-CNNs for arbitrary Lie groups. In our approach the differential structure of Lie groups is used to expand convolution kernels in a generic basis of B-splines that is defined on the Lie algebra. This leads to a flexible framework that enables localized, atrous, and deformable convolutions in G-CNNs by means of respectively localized, sparse and non-uniform B-spline expansions. The impact and potential of our approach is studied on two benchmark datasets: cancer detection in histopathology slides in which rotation equivariance plays a key role and facial landmark localization in which scale equivariance is important. In both cases, G-CNN architectures outperform their classical 2D counterparts and the added value of atrous and localized group convolutions is studied in detail.

Roto-Translation Covariant Convolutional Networks for Medical Image Analysis

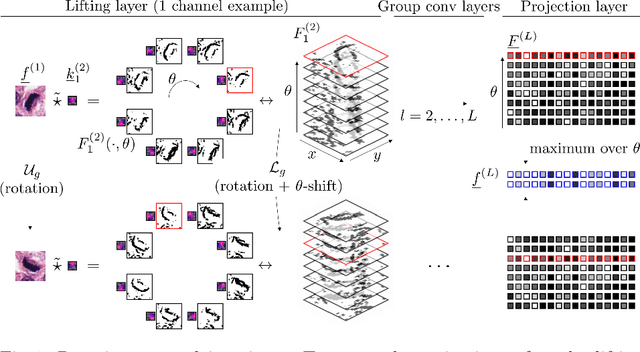
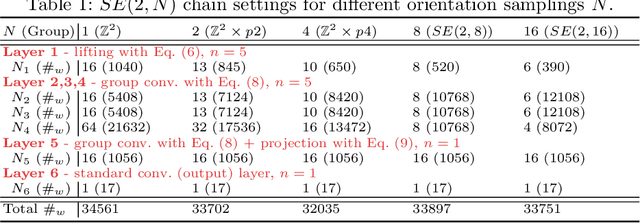
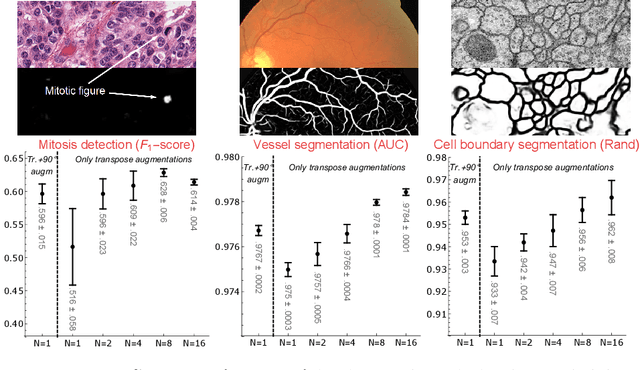
We propose a framework for rotation and translation covariant deep learning using $SE(2)$ group convolutions. The group product of the special Euclidean motion group $SE(2)$ describes how a concatenation of two roto-translations results in a net roto-translation. We encode this geometric structure into convolutional neural networks (CNNs) via $SE(2)$ group convolutional layers, which fit into the standard 2D CNN framework, and which allow to generically deal with rotated input samples without the need for data augmentation. We introduce three layers: a lifting layer which lifts a 2D (vector valued) image to an $SE(2)$-image, i.e., 3D (vector valued) data whose domain is $SE(2)$; a group convolution layer from and to an $SE(2)$-image; and a projection layer from an $SE(2)$-image to a 2D image. The lifting and group convolution layers are $SE(2)$ covariant (the output roto-translates with the input). The final projection layer, a maximum intensity projection over rotations, makes the full CNN rotation invariant. We show with three different problems in histopathology, retinal imaging, and electron microscopy that with the proposed group CNNs, state-of-the-art performance can be achieved, without the need for data augmentation by rotation and with increased performance compared to standard CNNs that do rely on augmentation.