Eric F. Lock
Multiple Linked Tensor Factorization
Feb 27, 2025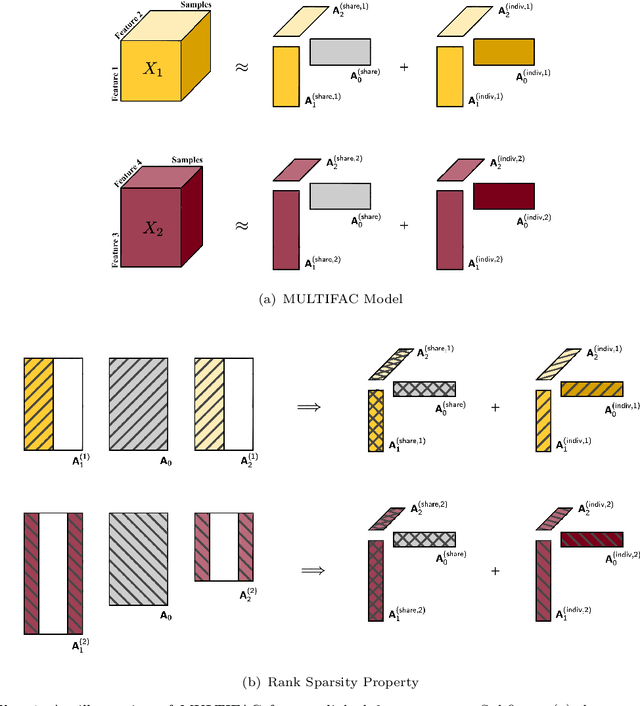
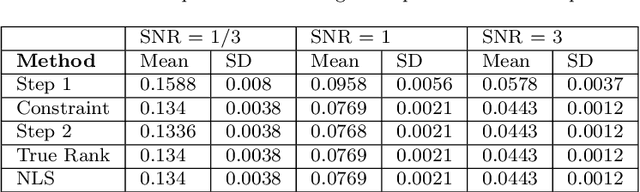
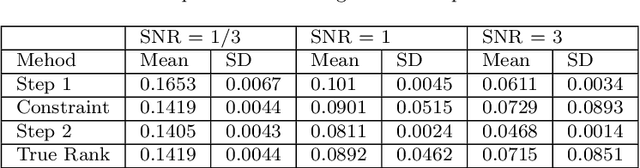
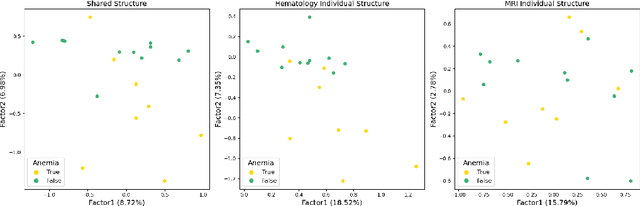
Abstract:In biomedical research and other fields, it is now common to generate high content data that are both multi-source and multi-way. Multi-source data are collected from different high-throughput technologies while multi-way data are collected over multiple dimensions, yielding multiple tensor arrays. Integrative analysis of these data sets is needed, e.g., to capture and synthesize different facets of complex biological systems. However, despite growing interest in multi-source and multi-way factorization techniques, methods that can handle data that are both multi-source and multi-way are limited. In this work, we propose a Multiple Linked Tensors Factorization (MULTIFAC) method extending the CANDECOMP/PARAFAC (CP) decomposition to simultaneously reduce the dimension of multiple multi-way arrays and approximate underlying signal. We first introduce a version of the CP factorization with L2 penalties on the latent factors, leading to rank sparsity. When extended to multiple linked tensors, the method automatically reveals latent components that are shared across data sources or individual to each data source. We also extend the decomposition algorithm to its expectation-maximization (EM) version to handle incomplete data with imputation. Extensive simulation studies are conducted to demonstrate MULTIFAC's ability to (i) approximate underlying signal, (ii) identify shared and unshared structures, and (iii) impute missing data. The approach yields an interpretable decomposition on multi-way multi-omics data for a study on early-life iron deficiency.
BAMITA: Bayesian Multiple Imputation for Tensor Arrays
Oct 30, 2024Abstract:Data increasingly take the form of a multi-way array, or tensor, in several biomedical domains. Such tensors are often incompletely observed. For example, we are motivated by longitudinal microbiome studies in which several timepoints are missing for several subjects. There is a growing literature on missing data imputation for tensors. However, existing methods give a point estimate for missing values without capturing uncertainty. We propose a multiple imputation approach for tensors in a flexible Bayesian framework, that yields realistic simulated values for missing entries and can propagate uncertainty through subsequent analyses. Our model uses efficient and widely applicable conjugate priors for a CANDECOMP/PARAFAC (CP) factorization, with a separable residual covariance structure. This approach is shown to perform well with respect to both imputation accuracy and uncertainty calibration, for scenarios in which either single entries or entire fibers of the tensor are missing. For two microbiome applications, it is shown to accurately capture uncertainty in the full microbiome profile at missing timepoints and used to infer trends in species diversity for the population. Documented R code to perform our multiple imputation approach is available at https://github.com/lockEF/MultiwayImputation .
Empirical Bayes Linked Matrix Decomposition
Aug 01, 2024Abstract:Data for several applications in diverse fields can be represented as multiple matrices that are linked across rows or columns. This is particularly common in molecular biomedical research, in which multiple molecular "omics" technologies may capture different feature sets (e.g., corresponding to rows in a matrix) and/or different sample populations (corresponding to columns). This has motivated a large body of work on integrative matrix factorization approaches that identify and decompose low-dimensional signal that is shared across multiple matrices or specific to a given matrix. We propose an empirical variational Bayesian approach to this problem that has several advantages over existing techniques, including the flexibility to accommodate shared signal over any number of row or column sets (i.e., bidimensional integration), an intuitive model-based objective function that yields appropriate shrinkage for the inferred signals, and a relatively efficient estimation algorithm with no tuning parameters. A general result establishes conditions for the uniqueness of the underlying decomposition for a broad family of methods that includes the proposed approach. For scenarios with missing data, we describe an associated iterative imputation approach that is novel for the single-matrix context and a powerful approach for "blockwise" imputation (in which an entire row or column is missing) in various linked matrix contexts. Extensive simulations show that the method performs very well under different scenarios with respect to recovering underlying low-rank signal, accurately decomposing shared and specific signals, and accurately imputing missing data. The approach is applied to gene expression and miRNA data from breast cancer tissue and normal breast tissue, for which it gives an informative decomposition of variation and outperforms alternative strategies for missing data imputation.
* 29 pages, 8 figures
Multiple Augmented Reduced Rank Regression for Pan-Cancer Analysis
Aug 30, 2023Abstract:Statistical approaches that successfully combine multiple datasets are more powerful, efficient, and scientifically informative than separate analyses. To address variation architectures correctly and comprehensively for high-dimensional data across multiple sample sets (i.e., cohorts), we propose multiple augmented reduced rank regression (maRRR), a flexible matrix regression and factorization method to concurrently learn both covariate-driven and auxiliary structured variation. We consider a structured nuclear norm objective that is motivated by random matrix theory, in which the regression or factorization terms may be shared or specific to any number of cohorts. Our framework subsumes several existing methods, such as reduced rank regression and unsupervised multi-matrix factorization approaches, and includes a promising novel approach to regression and factorization of a single dataset (aRRR) as a special case. Simulations demonstrate substantial gains in power from combining multiple datasets, and from parsimoniously accounting for all structured variation. We apply maRRR to gene expression data from multiple cancer types (i.e., pan-cancer) from TCGA, with somatic mutations as covariates. The method performs well with respect to prediction and imputation of held-out data, and provides new insights into mutation-driven and auxiliary variation that is shared or specific to certain cancer types.
Bayesian Simultaneous Factorization and Prediction Using Multi-Omic Data
Nov 30, 2022Abstract:Understanding of the pathophysiology of obstructive lung disease (OLD) is limited by available methods to examine the relationship between multi-omic molecular phenomena and clinical outcomes. Integrative factorization methods for multi-omic data can reveal latent patterns of variation describing important biological signal. However, most methods do not provide a framework for inference on the estimated factorization, simultaneously predict important disease phenotypes or clinical outcomes, nor accommodate multiple imputation. To address these gaps, we propose Bayesian Simultaneous Factorization (BSF). We use conjugate normal priors and show that the posterior mode of this model can be estimated by solving a structured nuclear norm-penalized objective that also achieves rank selection and motivates the choice of hyperparameters. We then extend BSF to simultaneously predict a continuous or binary response, termed Bayesian Simultaneous Factorization and Prediction (BSFP). BSF and BSFP accommodate concurrent imputation and full posterior inference for missing data, including "blockwise" missingness, and BSFP offers prediction of unobserved outcomes. We show via simulation that BSFP is competitive in recovering latent variation structure, as well as the importance of propagating uncertainty from the estimated factorization to prediction. We also study the imputation performance of BSF via simulation under missing-at-random and missing-not-at-random assumptions. Lastly, we use BSFP to predict lung function based on the bronchoalveolar lavage metabolome and proteome from a study of HIV-associated OLD. Our analysis reveals a distinct cluster of patients with OLD driven by shared metabolomic and proteomic expression patterns, as well as multi-omic patterns related to lung function decline. Software is freely available at https://github.com/sarahsamorodnitsky/BSFP .
Bayesian predictive modeling of multi-source multi-way data
Aug 05, 2022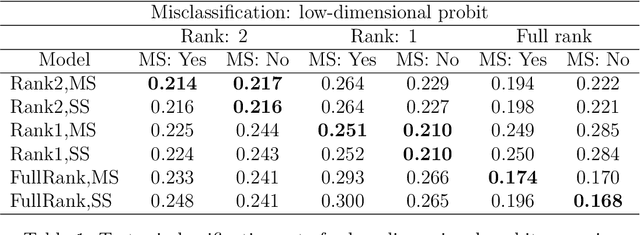
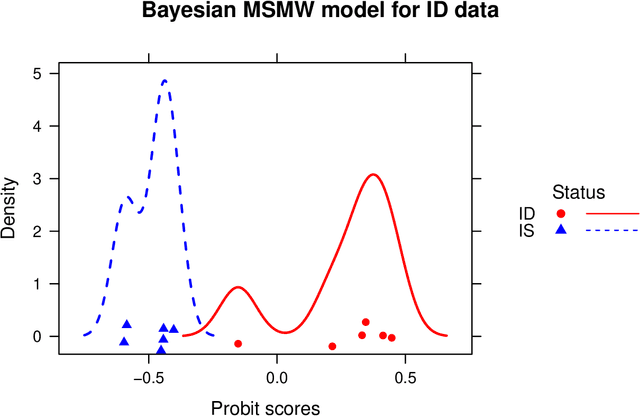
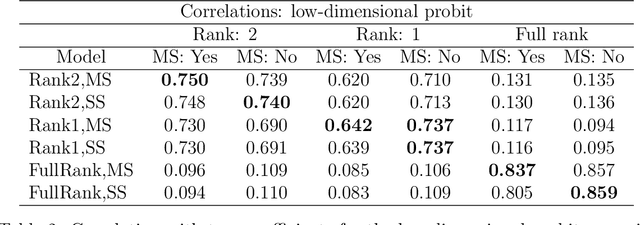
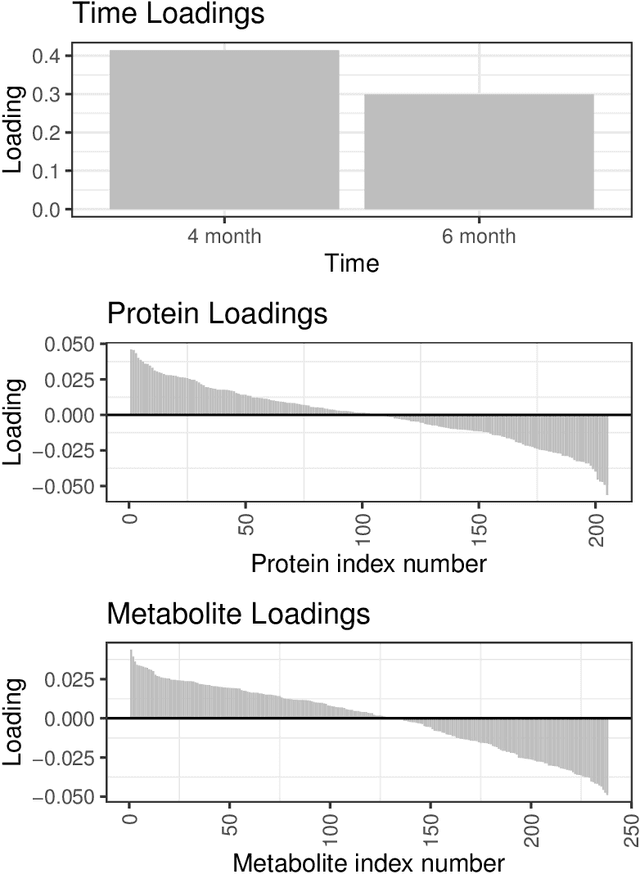
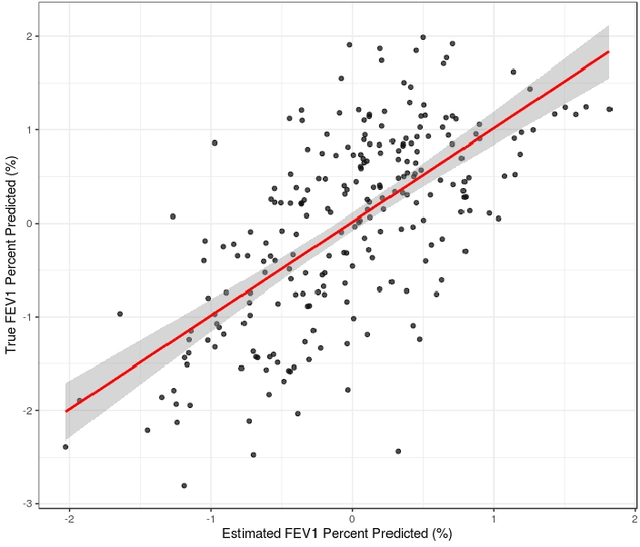
Abstract:We develop a Bayesian approach to predict a continuous or binary outcome from data that are collected from multiple sources with a multi-way (i.e.. multidimensional tensor) structure. As a motivating example we consider molecular data from multiple 'omics sources, each measured over multiple developmental time points, as predictors of early-life iron deficiency (ID) in a rhesus monkey model. We use a linear model with a low-rank structure on the coefficients to capture multi-way dependence and model the variance of the coefficients separately across each source to infer their relative contributions. Conjugate priors facilitate an efficient Gibbs sampling algorithm for posterior inference, assuming a continuous outcome with normal errors or a binary outcome with a probit link. Simulations demonstrate that our model performs as expected in terms of misclassification rates and correlation of estimated coefficients with true coefficients, with large gains in performance by incorporating multi-way structure and modest gains when accounting for differing signal sizes across the different sources. Moreover, it provides robust classification of ID monkeys for our motivating application. Software in the form of R code is available at https://github.com/BiostatsKim/BayesMSMW .
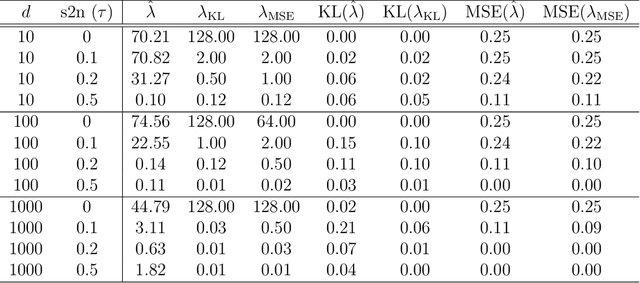
Multiway sparse distance weighted discrimination
Oct 11, 2021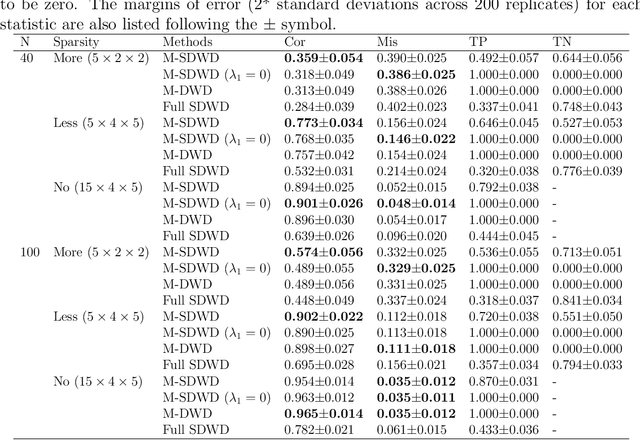
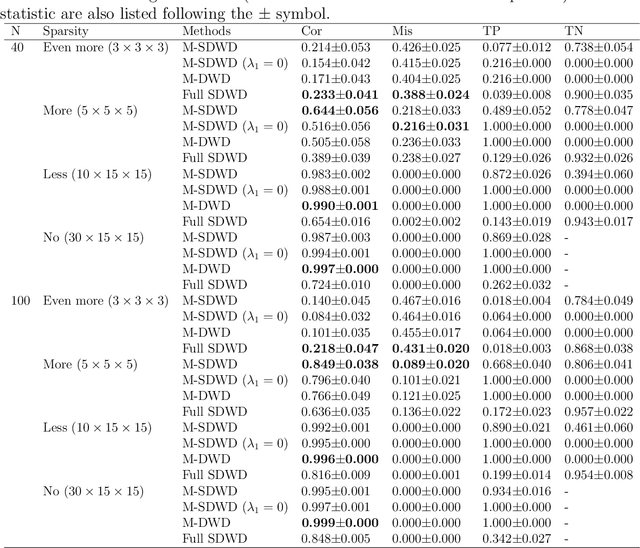
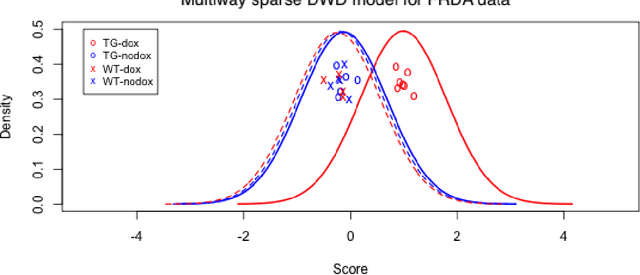
Abstract:Modern data often take the form of a multiway array. However, most classification methods are designed for vectors, i.e., 1-way arrays. Distance weighted discrimination (DWD) is a popular high-dimensional classification method that has been extended to the multiway context, with dramatic improvements in performance when data have multiway structure. However, the previous implementation of multiway DWD was restricted to classification of matrices, and did not account for sparsity. In this paper, we develop a general framework for multiway classification which is applicable to any number of dimensions and any degree of sparsity. We conducted extensive simulation studies, showing that our model is robust to the degree of sparsity and improves classification accuracy when the data have multiway structure. For our motivating application, magnetic resonance spectroscopy (MRS) was used to measure the abundance of several metabolites across multiple neurological regions and across multiple time points in a mouse model of Friedreich's ataxia, yielding a four-way data array. Our method reveals a robust and interpretable multi-region metabolomic signal that discriminates the groups of interest. We also successfully apply our method to gene expression time course data for multiple sclerosis treatment. An R implementation is available in the package MultiwayClassification at http://github.com/lockEF/MultiwayClassification .
sJIVE: Supervised Joint and Individual Variation Explained
Feb 26, 2021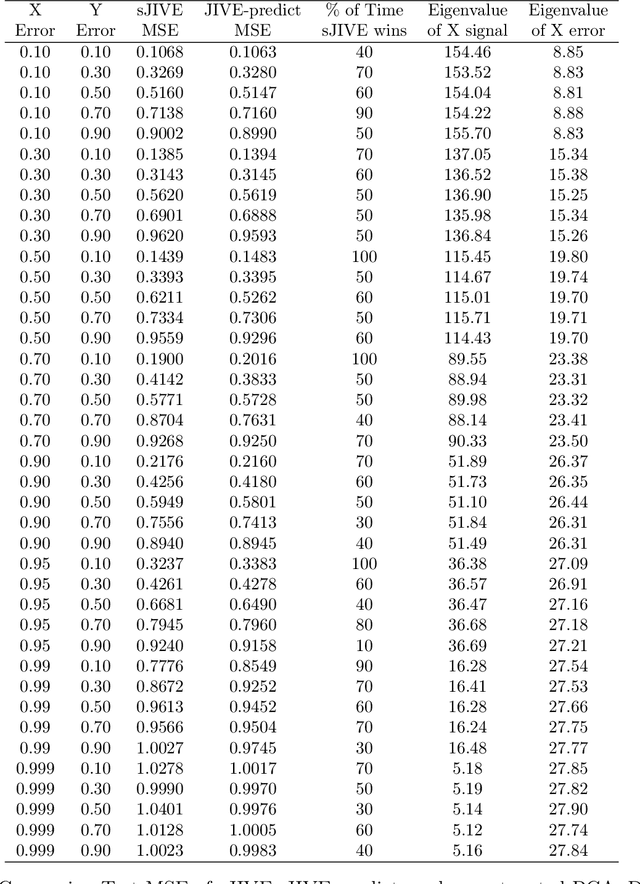


Abstract:Analyzing multi-source data, which are multiple views of data on the same subjects, has become increasingly common in molecular biomedical research. Recent methods have sought to uncover underlying structure and relationships within and/or between the data sources, and other methods have sought to build a predictive model for an outcome using all sources. However, existing methods that do both are presently limited because they either (1) only consider data structure shared by all datasets while ignoring structures unique to each source, or (2) they extract underlying structures first without consideration to the outcome. We propose a method called supervised joint and individual variation explained (sJIVE) that can simultaneously (1) identify shared (joint) and source-specific (individual) underlying structure and (2) build a linear prediction model for an outcome using these structures. These two components are weighted to compromise between explaining variation in the multi-source data and in the outcome. Simulations show sJIVE to outperform existing methods when large amounts of noise are present in the multi-source data. An application to data from the COPDGene study reveals gene expression and proteomic patterns that are predictive of lung function. Functions to perform sJIVE are included in the R.JIVE package, available online at http://github.com/lockEF/r.jive .
Bayesian Distance Weighted Discrimination
Oct 07, 2020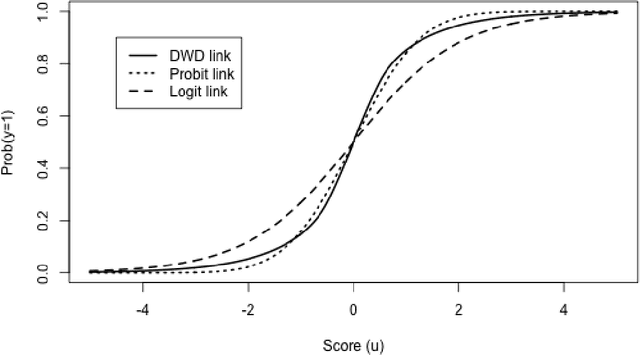
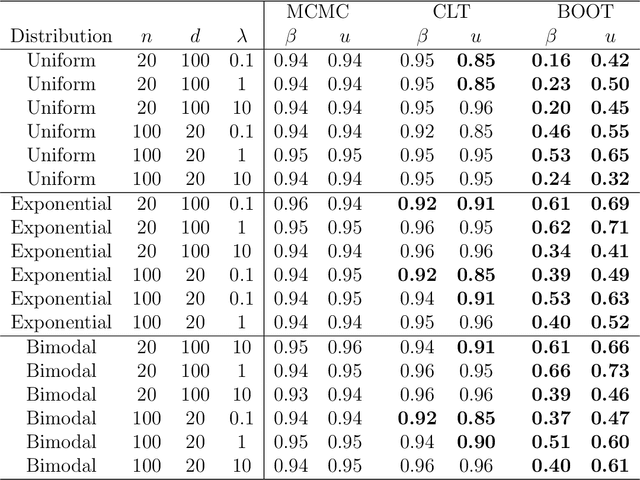
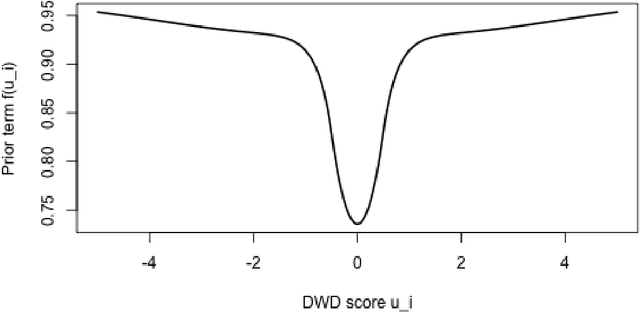
Abstract:Distance weighted discrimination (DWD) is a linear discrimination method that is particularly well-suited for classification tasks with high-dimensional data. The DWD coefficients minimize an intuitive objective function, which can solved very efficiently using state-of-the-art optimization techniques. However, DWD has not yet been cast into a model-based framework for statistical inference. In this article we show that DWD identifies the mode of a proper Bayesian posterior distribution, that results from a particular link function for the class probabilities and a shrinkage-inducing proper prior distribution on the coefficients. We describe a relatively efficient Markov chain Monte Carlo (MCMC) algorithm to simulate from the true posterior under this Bayesian framework. We show that the posterior is asymptotically normal and derive the mean and covariance matrix of its limiting distribution. Through several simulation studies and an application to breast cancer genomics we demonstrate how the Bayesian approach to DWD can be used to (1) compute well-calibrated posterior class probabilities, (2) assess uncertainty in the DWD coefficients and resulting sample scores, (3) improve power via semi-supervised analysis when not all class labels are available, and (4) automatically determine a penalty tuning parameter within the model-based framework. R code to perform Bayesian DWD is available at https://github.com/lockEF/BayesianDWD .
Bidimensional linked matrix factorization for pan-omics pan-cancer analysis
Feb 07, 2020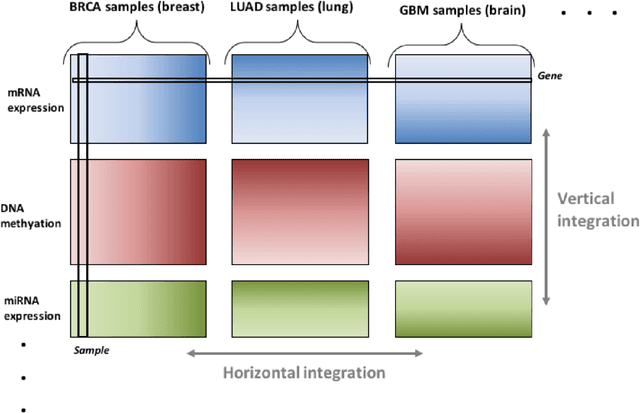
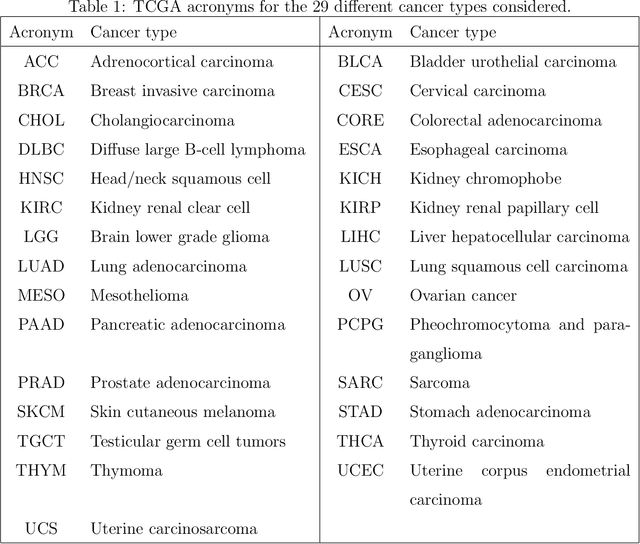
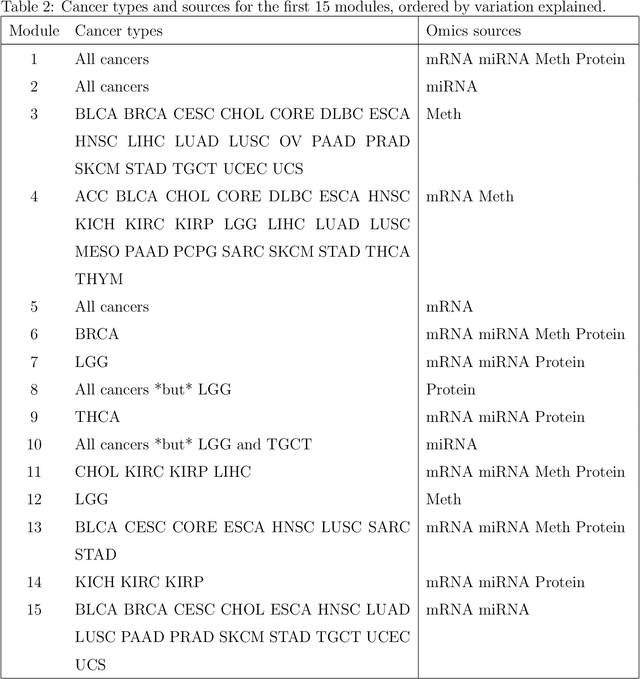
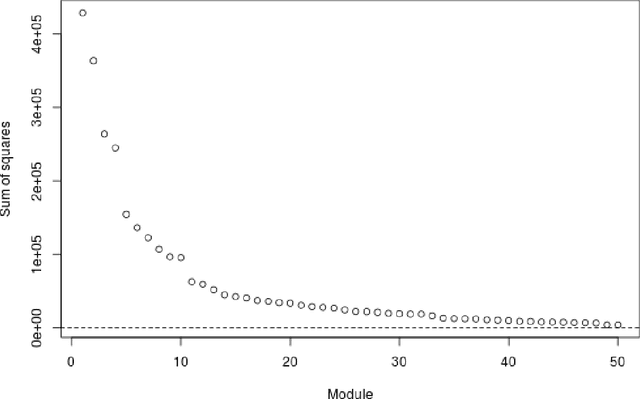
Abstract:Several modern applications require the integration of multiple large data matrices that have shared rows and/or columns. For example, cancer studies that integrate multiple omics platforms across multiple types of cancer, pan-omics pan-cancer analysis, have extended our knowledge of molecular heterogenity beyond what was observed in single tumor and single platform studies. However, these studies have been limited by available statistical methodology. We propose a flexible approach to the simultaneous factorization and decomposition of variation across such bidimensionally linked matrices, BIDIFAC+. This decomposes variation into a series of low-rank components that may be shared across any number of row sets (e.g., omics platforms) or column sets (e.g., cancer types). This builds on a growing literature for the factorization and decomposition of linked matrices, which has primarily focused on multiple matrices that are linked in one dimension (rows or columns) only. Our objective function extends nuclear norm penalization, is motivated by random matrix theory, gives an identifiable decomposition under relatively mild conditions, and can be shown to give the mode of a Bayesian posterior distribution. We apply BIDIFAC+ to pan-omics pan-cancer data from TCGA, identifying shared and specific modes of variability across 4 different omics platforms and 29 different cancer types.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge