Bidimensional linked matrix factorization for pan-omics pan-cancer analysis

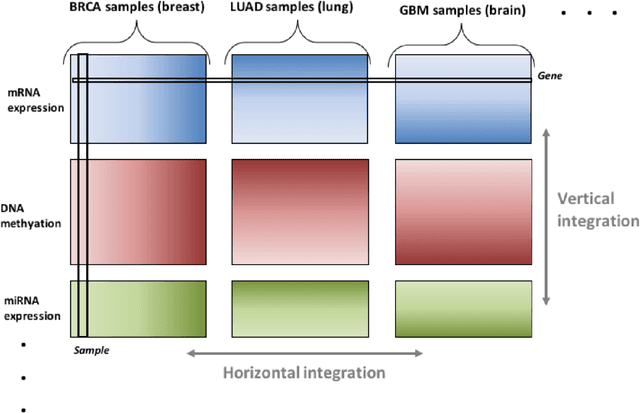
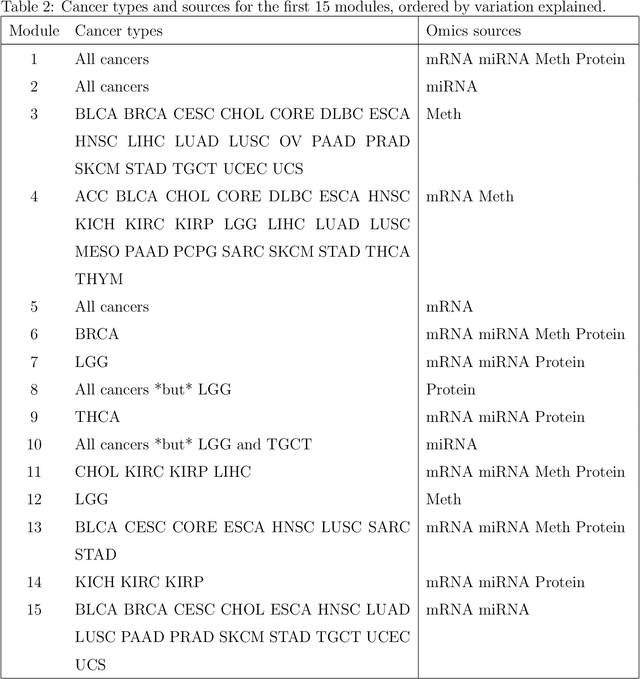
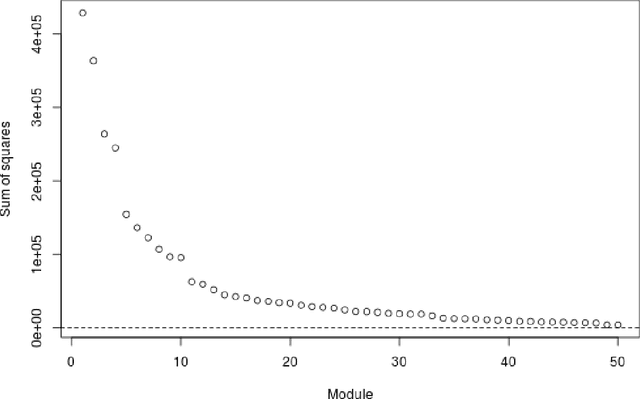
Several modern applications require the integration of multiple large data matrices that have shared rows and/or columns. For example, cancer studies that integrate multiple omics platforms across multiple types of cancer, pan-omics pan-cancer analysis, have extended our knowledge of molecular heterogenity beyond what was observed in single tumor and single platform studies. However, these studies have been limited by available statistical methodology. We propose a flexible approach to the simultaneous factorization and decomposition of variation across such bidimensionally linked matrices, BIDIFAC+. This decomposes variation into a series of low-rank components that may be shared across any number of row sets (e.g., omics platforms) or column sets (e.g., cancer types). This builds on a growing literature for the factorization and decomposition of linked matrices, which has primarily focused on multiple matrices that are linked in one dimension (rows or columns) only. Our objective function extends nuclear norm penalization, is motivated by random matrix theory, gives an identifiable decomposition under relatively mild conditions, and can be shown to give the mode of a Bayesian posterior distribution. We apply BIDIFAC+ to pan-omics pan-cancer data from TCGA, identifying shared and specific modes of variability across 4 different omics platforms and 29 different cancer types.

Integrative Factorization of Bidimensionally Linked Matrices

Advances in molecular "omics'" technologies have motivated new methodology for the integration of multiple sources of high-content biomedical data. However, most statistical methods for integrating multiple data matrices only consider data shared vertically (one cohort on multiple platforms) or horizontally (different cohorts on a single platform). This is limiting for data that take the form of bidimensionally linked matrices (e.g., multiple cohorts measured on multiple platforms), which are increasingly common in large-scale biomedical studies. In this paper, we propose BIDIFAC (Bidimensional Integrative Factorization) for integrative dimension reduction and signal approximation of bidimensionally linked data matrices. Our method factorizes the data into (i) globally shared, (ii) row-shared, (iii) column-shared, and (iv) single-matrix structural components, facilitating the investigation of shared and unique patterns of variability. For estimation we use a penalized objective function that extends the nuclear norm penalization for a single matrix. As an alternative to the complicated rank selection problem, we use results from random matrix theory to choose tuning parameters. We apply our method to integrate two genomics platforms (mRNA and miRNA expression) across two sample cohorts (tumor samples and normal tissue samples) using the breast cancer data from TCGA. We provide R code for fitting BIDIFAC, imputing missing values, and generating simulated data.