Erhan Bayraktar
Entropy-Based Dimension-Free Convergence and Loss-Adaptive Schedules for Diffusion Models
Jan 29, 2026Abstract:Diffusion generative models synthesize samples by discretizing reverse-time dynamics driven by a learned score (or denoiser). Existing convergence analyses of diffusion models typically scale at least linearly with the ambient dimension, and sharper rates often depend on intrinsic-dimension assumptions or other geometric restrictions on the target distribution. We develop an alternative, information-theoretic approach to dimension-free convergence that avoids any geometric assumptions. Under mild assumptions on the target distribution, we bound KL divergence between the target and generated distributions by $O(H^2/K)$ (up to endpoint factors), where $H$ is the Shannon entropy and $K$ is the number of sampling steps. Moreover, using a reformulation of the KL divergence, we propose a Loss-Adaptive Schedule (LAS) for efficient discretization of reverse SDE which is lightweight and relies only on the training loss, requiring no post-training heavy computation. Empirically, LAS improves sampling quality over common heuristic schedules.
Deep Neural Operator Learning for Probabilistic Models
Nov 10, 2025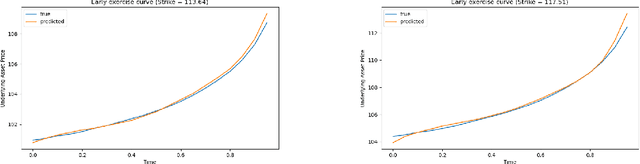
Abstract:We propose a deep neural-operator framework for a general class of probability models. Under global Lipschitz conditions on the operator over the entire Euclidean space-and for a broad class of probabilistic models-we establish a universal approximation theorem with explicit network-size bounds for the proposed architecture. The underlying stochastic processes are required only to satisfy integrability and general tail-probability conditions. We verify these assumptions for both European and American option-pricing problems within the forward-backward SDE (FBSDE) framework, which in turn covers a broad class of operators arising from parabolic PDEs, with or without free boundaries. Finally, we present a numerical example for a basket of American options, demonstrating that the learned model produces optimal stopping boundaries for new strike prices without retraining.
Fitted Value Iteration Methods for Bicausal Optimal Transport
Jun 22, 2023Abstract:We develop a fitted value iteration (FVI) method to compute bicausal optimal transport (OT) where couplings have an adapted structure. Based on the dynamic programming formulation, FVI adopts a function class to approximate the value functions in bicausal OT. Under the concentrability condition and approximate completeness assumption, we prove the sample complexity using (local) Rademacher complexity. Furthermore, we demonstrate that multilayer neural networks with appropriate structures satisfy the crucial assumptions required in sample complexity proofs. Numerical experiments reveal that FVI outperforms linear programming and adapted Sinkhorn methods in scalability as the time horizon increases, while still maintaining acceptable accuracy.
Deep Signature Algorithm for Path-Dependent American option pricing
Nov 21, 2022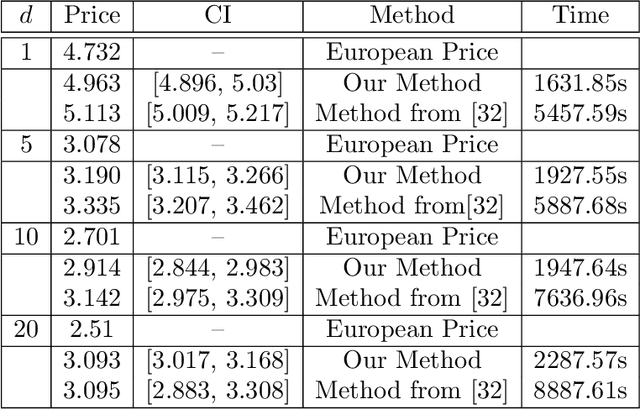
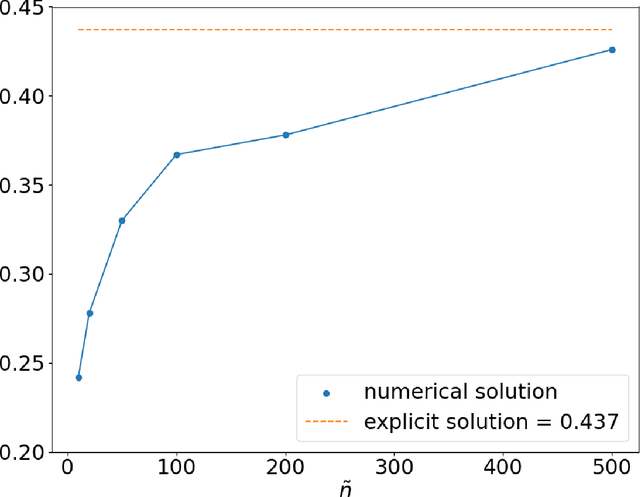
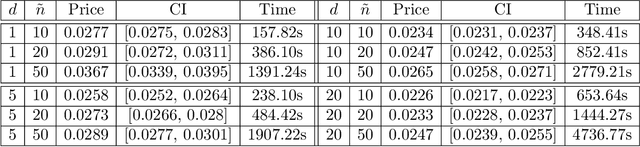
Abstract:In this work, we study the deep signature algorithms for path-dependent FBSDEs with reflections. We follow the backward scheme in [Hur\'e-Pham-Warin. Mathematics of Computation 89, no. 324 (2020)] for state-dependent FBSDEs with reflections, and combine it with the signature layer to solve American type option pricing problems while the payoff function depends on the whole paths of the underlying forward stock process. We prove the convergence analysis of our numerical algorithm and provide numerical example for Amerasian option under the Black-Scholes model.
A PDE approach for regret bounds under partial monitoring
Sep 02, 2022Abstract:In this paper, we study a learning problem in which a forecaster only observes partial information. By properly rescaling the problem, we heuristically derive a limiting PDE on Wasserstein space which characterizes the asymptotic behavior of the regret of the forecaster. Using a verification type argument, we show that the problem of obtaining regret bounds and efficient algorithms can be tackled by finding appropriate smooth sub/supersolutions of this parabolic PDE.
Prediction against limited adversary
Oct 31, 2020Abstract:We study the problem of prediction with expert advice with adversarial corruption where the adversary can at most corrupt one expert. Using tools from viscosity theory, we characterize the long-time behavior of the value function of the game between the forecaster and the adversary. We provide lower and upper bounds for the growth rate of regret without relying on a comparison result. We show that depending on the description of regret, the limiting behavior of the game can significantly differ.
Malicious Experts versus the multiplicative weights algorithm in online prediction
Mar 18, 2020Abstract:We consider a prediction problem with two experts and a forecaster. We assume that one of the experts is honest and makes correct prediction with probability $\mu$ at each round. The other one is malicious, who knows true outcomes at each round and makes predictions in order to maximize the loss of the forecaster. Assuming the forecaster adopts the classical multiplicative weights algorithm, we find upper and lower bounds for the value function of the malicious expert. Our results imply that the multiplicative weights algorithm cannot resist the corruption of malicious experts. We also show that an adaptive multiplicative weights algorithm is asymptotically optimal for the forecaster, and hence more resistant to the corruption of malicious experts.
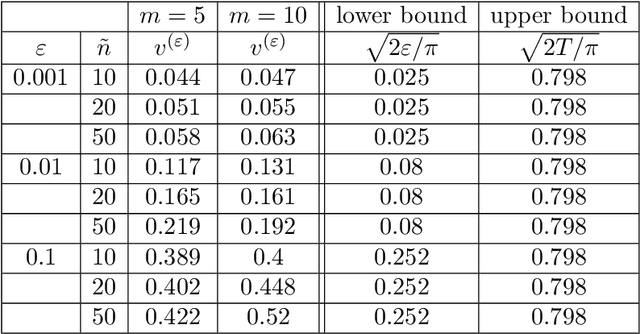
Finite-Time 4-Expert Prediction Problem
Dec 03, 2019
Abstract:We explicitly solve the nonlinear PDE that is the continuous limit of dynamic programming of \emph{expert prediction problem} in finite horizon setting with $N=4$ experts. The \emph{expert prediction problem} is formulated as a zero sum game between a player and an adversary. By showing that the solution is $\mathcal{C}^2$, we are able to show that the strategies conjectured in arXiv:1409.3040G form an asymptotic Nash equilibrium. We also prove the "Finite vs Geometric regret" conjecture proposed in arXiv:1409.3040G for $N=4$, and and show that this conjecture in fact follows from the conjecture that the comb strategies are optimal.
On the Adversarial Robustness of Multivariate Robust Estimation
Mar 27, 2019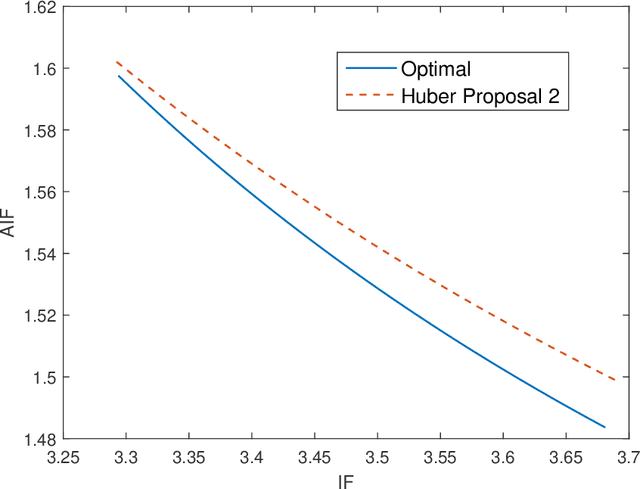
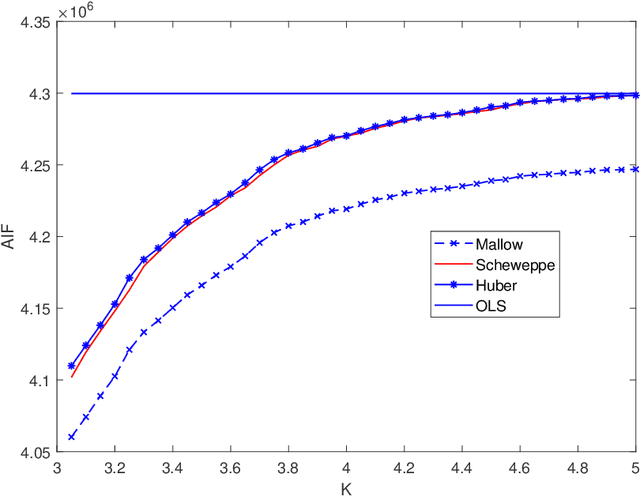
Abstract:In this paper, we investigate the adversarial robustness of multivariate $M$-Estimators. In the considered model, after observing the whole dataset, an adversary can modify all data points with the goal of maximizing inference errors. We use adversarial influence function (AIF) to measure the asymptotic rate at which the adversary can change the inference result. We first characterize the adversary's optimal modification strategy and its corresponding AIF. From the defender's perspective, we would like to design an estimator that has a small AIF. For the case of joint location and scale estimation problem, we characterize the optimal $M$-estimator that has the smallest AIF. We further identify a tradeoff between robustness against adversarial modifications and robustness against outliers, and derive the optimal $M$-estimator that achieves the best tradeoff.
On the asymptotic optimality of the comb strategy for prediction with expert advice
Feb 06, 2019Abstract:For the problem of prediction with expert advice in the adversarial setting with geometric stopping, we compute the exact leading order expansion for the long time behavior of the value function. Then, we use this expansion to prove that as conjectured in Gravin et al. [12], the comb strategies are indeed asymptotically optimal for the adversary in the case of 4 experts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge