Neural Operators Can Play Dynamic Stackelberg Games

Dynamic Stackelberg games are a broad class of two-player games in which the leader acts first, and the follower chooses a response strategy to the leader's strategy. Unfortunately, only stylized Stackelberg games are explicitly solvable since the follower's best-response operator (as a function of the control of the leader) is typically analytically intractable. This paper addresses this issue by showing that the \textit{follower's best-response operator} can be approximately implemented by an \textit{attention-based neural operator}, uniformly on compact subsets of adapted open-loop controls for the leader. We further show that the value of the Stackelberg game where the follower uses the approximate best-response operator approximates the value of the original Stackelberg game. Our main result is obtained using our universal approximation theorem for attention-based neural operators between spaces of square-integrable adapted stochastic processes, as well as stability results for a general class of Stackelberg games.

A PDE approach for regret bounds under partial monitoring

In this paper, we study a learning problem in which a forecaster only observes partial information. By properly rescaling the problem, we heuristically derive a limiting PDE on Wasserstein space which characterizes the asymptotic behavior of the regret of the forecaster. Using a verification type argument, we show that the problem of obtaining regret bounds and efficient algorithms can be tackled by finding appropriate smooth sub/supersolutions of this parabolic PDE.

Prediction against limited adversary

We study the problem of prediction with expert advice with adversarial corruption where the adversary can at most corrupt one expert. Using tools from viscosity theory, we characterize the long-time behavior of the value function of the game between the forecaster and the adversary. We provide lower and upper bounds for the growth rate of regret without relying on a comparison result. We show that depending on the description of regret, the limiting behavior of the game can significantly differ.

Finite-Time 4-Expert Prediction Problem

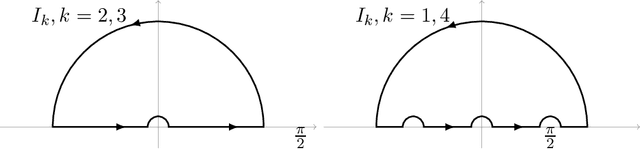
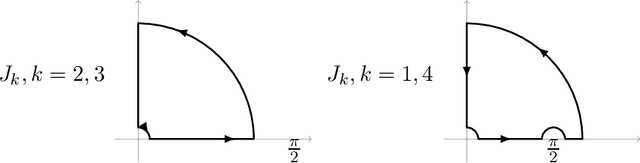
We explicitly solve the nonlinear PDE that is the continuous limit of dynamic programming of \emph{expert prediction problem} in finite horizon setting with $N=4$ experts. The \emph{expert prediction problem} is formulated as a zero sum game between a player and an adversary. By showing that the solution is $\mathcal{C}^2$, we are able to show that the strategies conjectured in arXiv:1409.3040G form an asymptotic Nash equilibrium. We also prove the "Finite vs Geometric regret" conjecture proposed in arXiv:1409.3040G for $N=4$, and and show that this conjecture in fact follows from the conjecture that the comb strategies are optimal.

On the asymptotic optimality of the comb strategy for prediction with expert advice

For the problem of prediction with expert advice in the adversarial setting with geometric stopping, we compute the exact leading order expansion for the long time behavior of the value function. Then, we use this expansion to prove that as conjectured in Gravin et al. [12], the comb strategies are indeed asymptotically optimal for the adversary in the case of 4 experts.