On the Adversarial Robustness of Multivariate Robust Estimation
Paper and Code
Mar 27, 2019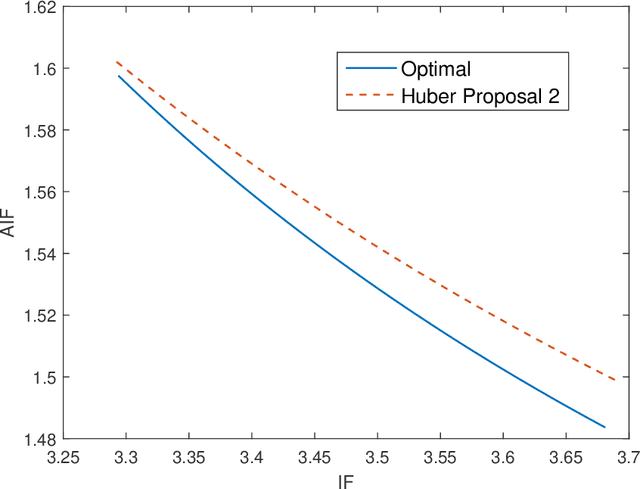
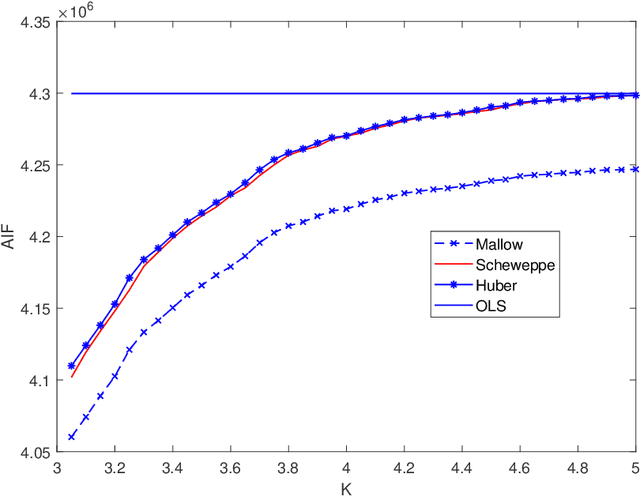
In this paper, we investigate the adversarial robustness of multivariate $M$-Estimators. In the considered model, after observing the whole dataset, an adversary can modify all data points with the goal of maximizing inference errors. We use adversarial influence function (AIF) to measure the asymptotic rate at which the adversary can change the inference result. We first characterize the adversary's optimal modification strategy and its corresponding AIF. From the defender's perspective, we would like to design an estimator that has a small AIF. For the case of joint location and scale estimation problem, we characterize the optimal $M$-estimator that has the smallest AIF. We further identify a tradeoff between robustness against adversarial modifications and robustness against outliers, and derive the optimal $M$-estimator that achieves the best tradeoff.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge