Fitted Value Iteration Methods for Bicausal Optimal Transport

We develop a fitted value iteration (FVI) method to compute bicausal optimal transport (OT) where couplings have an adapted structure. Based on the dynamic programming formulation, FVI adopts a function class to approximate the value functions in bicausal OT. Under the concentrability condition and approximate completeness assumption, we prove the sample complexity using (local) Rademacher complexity. Furthermore, we demonstrate that multilayer neural networks with appropriate structures satisfy the crucial assumptions required in sample complexity proofs. Numerical experiments reveal that FVI outperforms linear programming and adapted Sinkhorn methods in scalability as the time horizon increases, while still maintaining acceptable accuracy.

Distributionally robust risk evaluation with causality constraint and structural information

This work studies distributionally robust evaluation of expected function values over temporal data. A set of alternative measures is characterized by the causal optimal transport. We prove the strong duality and recast the causality constraint as minimization over an infinite-dimensional test function space. We approximate test functions by neural networks and prove the sample complexity with Rademacher complexity. Moreover, when structural information is available to further restrict the ambiguity set, we prove the dual formulation and provide efficient optimization methods. Simulation on stochastic volatility and empirical analysis on stock indices demonstrate that our framework offers an attractive alternative to the classic optimal transport formulation.

Understanding algorithmic collusion with experience replay

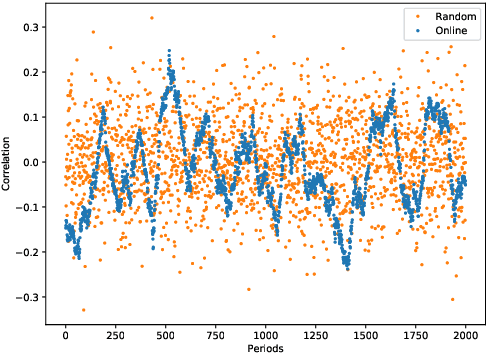
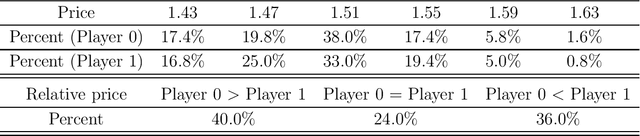
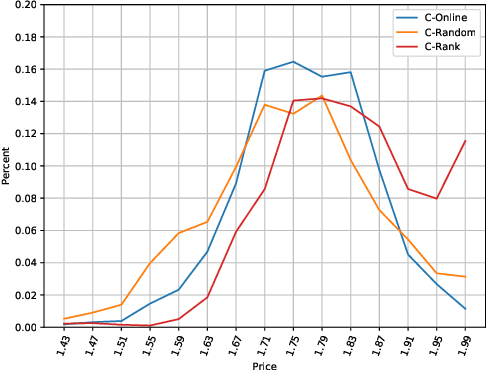
In an infinitely repeated pricing game, pricing algorithms based on artificial intelligence (Q-learning) may consistently learn to charge supra-competitive prices even without communication. Although concerns on algorithmic collusion have arisen, little is known on underlying factors. In this work, we experimentally analyze the dynamics of algorithms with three variants of experience replay. Algorithmic collusion still has roots in human preferences. Randomizing experience yields prices close to the static Bertrand equilibrium and higher prices are easily restored by favoring the latest experience. Moreover, relative performance concerns also stabilize the collusion. Finally, we investigate the scenarios with heterogeneous agents and test robustness on various factors.