Early-Exit meets Model-Distributed Inference at Edge Networks

Distributed inference techniques can be broadly classified into data-distributed and model-distributed schemes. In data-distributed inference (DDI), each worker carries the entire deep neural network (DNN) model but processes only a subset of the data. However, feeding the data to workers results in high communication costs, especially when the data is large. An emerging paradigm is model-distributed inference (MDI), where each worker carries only a subset of DNN layers. In MDI, a source device that has data processes a few layers of DNN and sends the output to a neighboring device, i.e., offloads the rest of the layers. This process ends when all layers are processed in a distributed manner. In this paper, we investigate the design and development of MDI with early-exit, which advocates that there is no need to process all the layers of a model for some data to reach the desired accuracy, i.e., we can exit the model without processing all the layers if target accuracy is reached. We design a framework MDI-Exit that adaptively determines early-exit and offloading policies as well as data admission at the source. Experimental results on a real-life testbed of NVIDIA Nano edge devices show that MDI-Exit processes more data when accuracy is fixed and results in higher accuracy for the fixed data rate.

Memorization Capacity of Neural Networks with Conditional Computation

Many empirical studies have demonstrated the performance benefits of conditional computation in neural networks, including reduced inference time and power consumption. We study the fundamental limits of neural conditional computation from the perspective of memorization capacity. For Rectified Linear Unit (ReLU) networks without conditional computation, it is known that memorizing a collection of $n$ input-output relationships can be accomplished via a neural network with $O(\sqrt{n})$ neurons. Calculating the output of this neural network can be accomplished using $O(\sqrt{n})$ elementary arithmetic operations of additions, multiplications and comparisons for each input. Using a conditional ReLU network, we show that the same task can be accomplished using only $O(\log n)$ operations per input. This represents an almost exponential improvement as compared to networks without conditional computation. We also show that the $\Theta(\log n)$ rate is the best possible. Our achievability result utilizes a general methodology to synthesize a conditional network out of an unconditional network in a computationally-efficient manner, bridging the gap between unconditional and conditional architectures.

Class Based Thresholding in Early Exit Semantic Segmentation Networks

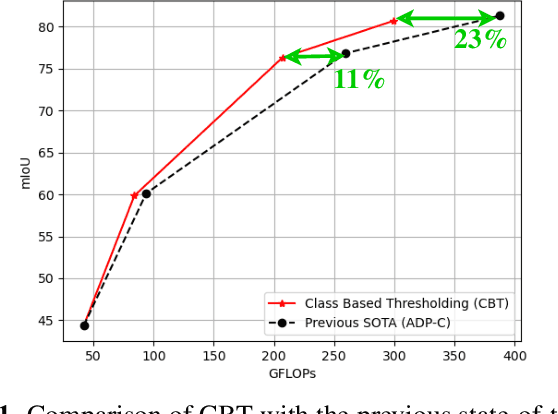
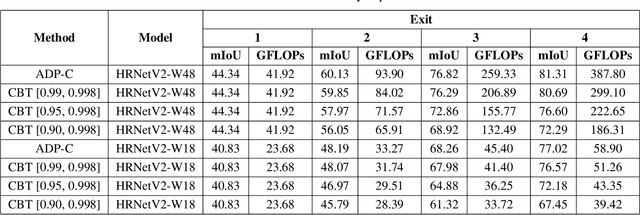
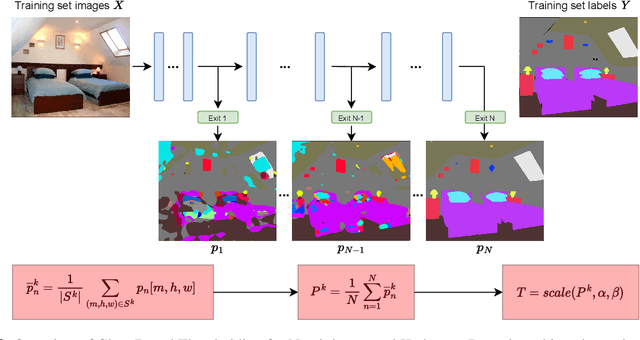
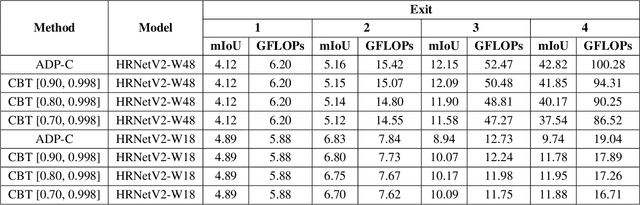
We propose Class Based Thresholding (CBT) to reduce the computational cost of early exit semantic segmentation models while preserving the mean intersection over union (mIoU) performance. A key idea of CBT is to exploit the naturally-occurring neural collapse phenomenon. Specifically, by calculating the mean prediction probabilities of each class in the training set, CBT assigns different masking threshold values to each class, so that the computation can be terminated sooner for pixels belonging to easy-to-predict classes. We show the effectiveness of CBT on Cityscapes and ADE20K datasets. CBT can reduce the computational cost by $23\%$ compared to the previous state-of-the-art early exit models.

Pruning Early Exit Networks

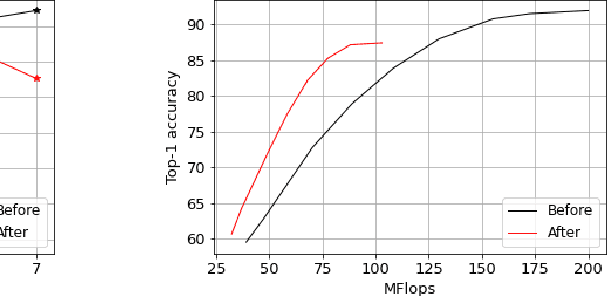
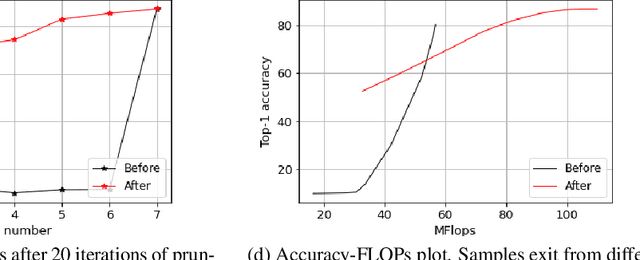
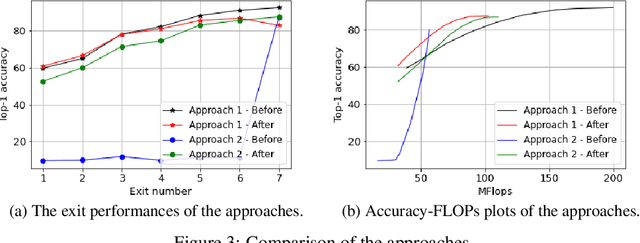
Deep learning models that perform well often have high computational costs. In this paper, we combine two approaches that try to reduce the computational cost while keeping the model performance high: pruning and early exit networks. We evaluate two approaches of pruning early exit networks: (1) pruning the entire network at once, (2) pruning the base network and additional linear classifiers in an ordered fashion. Experimental results show that pruning the entire network at once is a better strategy in general. However, at high accuracy rates, the two approaches have a similar performance, which implies that the processes of pruning and early exit can be separated without loss of optimality.

Federated Momentum Contrastive Clustering

We present federated momentum contrastive clustering (FedMCC), a learning framework that can not only extract discriminative representations over distributed local data but also perform data clustering. In FedMCC, a transformed data pair passes through both the online and target networks, resulting in four representations over which the losses are determined. The resulting high-quality representations generated by FedMCC can outperform several existing self-supervised learning methods for linear evaluation and semi-supervised learning tasks. FedMCC can easily be adapted to ordinary centralized clustering through what we call momentum contrastive clustering (MCC). We show that MCC achieves state-of-the-art clustering accuracy results in certain datasets such as STL-10 and ImageNet-10. We also present a method to reduce the memory footprint of our clustering schemes.

Multiplication-Avoiding Variant of Power Iteration with Applications

Power iteration is a fundamental algorithm in data analysis. It extracts the eigenvector corresponding to the largest eigenvalue of a given matrix. Applications include ranking algorithms, recommendation systems, principal component analysis (PCA), among many others. In this paper, We introduce multiplication-avoiding power iteration (MAPI), which replaces the standard $\ell_2$-inner products that appear at the regular power iteration (RPI) with multiplication-free vector products which are Mercer-type kernel operations related with the $\ell_1$ norm. Precisely, for an $n\times n$ matrix, MAPI requires $n$ multiplications, while RPI needs $n^2$ multiplications per iteration. Therefore, MAPI provides a significant reduction of the number of multiplication operations, which are known to be costly in terms of energy consumption. We provide applications of MAPI to PCA-based image reconstruction as well as to graph-based ranking algorithms. When compared to RPI, MAPI not only typically converges much faster, but also provides superior performance.

Robust Principal Component Analysis Using a Novel Kernel Related with the L1-Norm

We consider a family of vector dot products that can be implemented using sign changes and addition operations only. The dot products are energy-efficient as they avoid the multiplication operation entirely. Moreover, the dot products induce the $\ell_1$-norm, thus providing robustness to impulsive noise. First, we analytically prove that the dot products yield symmetric, positive semi-definite generalized covariance matrices, thus enabling principal component analysis (PCA). Moreover, the generalized covariance matrices can be constructed in an Energy Efficient (EEF) manner due to the multiplication-free property of the underlying vector products. We present image reconstruction examples in which our EEF PCA method result in the highest peak signal-to-noise ratios compared to the ordinary $\ell_2$-PCA and the recursive $\ell_1$-PCA.

Class Means as an Early Exit Decision Mechanism

State-of-the-art neural networks with early exit mechanisms often need considerable amount of training and fine-tuning to achieve good performance with low computational cost. We propose a novel early exit technique based on the class means of samples. Unlike most existing schemes, our method does not require gradient-based training of internal classifiers. This makes our method particularly useful for neural network training in low-power devices, as in wireless edge networks. In particular, given a fixed training time budget, our scheme achieves higher accuracy as compared to existing early exit mechanisms. Moreover, if there are no limitations on the training time budget, our method can be combined with an existing early exit scheme to boost its performance, achieving a better trade-off between computational cost and network accuracy.

Quantizing Multiple Sources to a Common Cluster Center: An Asymptotic Analysis

We consider quantizing an $Ld$-dimensional sample, which is obtained by concatenating $L$ vectors from datasets of $d$-dimensional vectors, to a $d$-dimensional cluster center. The distortion measure is the weighted sum of $r$th powers of the distances between the cluster center and the samples. For $L=1$, one recovers the ordinary center based clustering formulation. The general case $L>1$ appears when one wishes to cluster a dataset through $L$ noisy observations of each of its members. We find a formula for the average distortion performance in the asymptotic regime where the number of cluster centers are large. We also provide an algorithm to numerically optimize the cluster centers and verify our analytical results on real and artificial datasets. In terms of faithfulness to the original (noiseless) dataset, our clustering approach outperforms the naive approach that relies on quantizing the $Ld$-dimensional noisy observation vectors to $Ld$-dimensional centers.

A Generalization of Principal Component Analysis

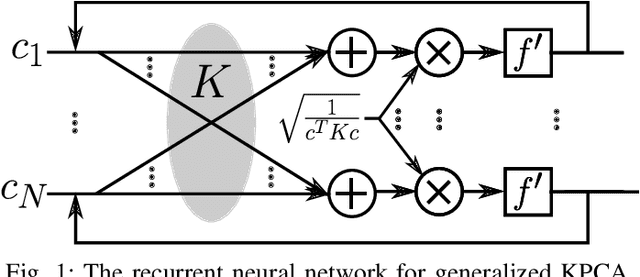
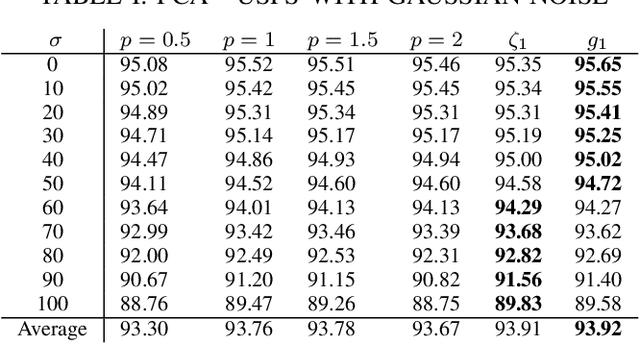
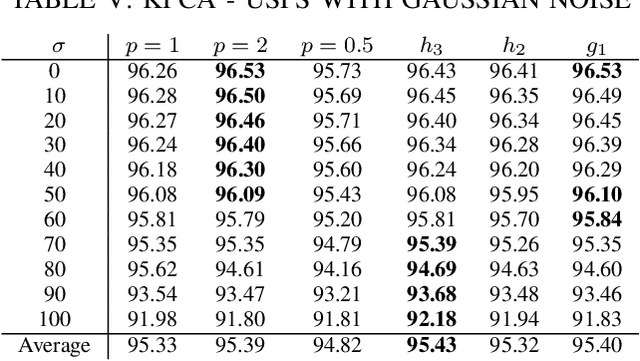
Conventional principal component analysis (PCA) finds a principal vector that maximizes the sum of second powers of principal components. We consider a generalized PCA that aims at maximizing the sum of an arbitrary convex function of principal components. We present a gradient ascent algorithm to solve the problem. For the kernel version of generalized PCA, we show that the solutions can be obtained as fixed points of a simple single-layer recurrent neural network. We also evaluate our algorithms on different datasets.