Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Samuele Battaglino
A Generalization of Principal Component Analysis
Nov 15, 2019Figures and Tables: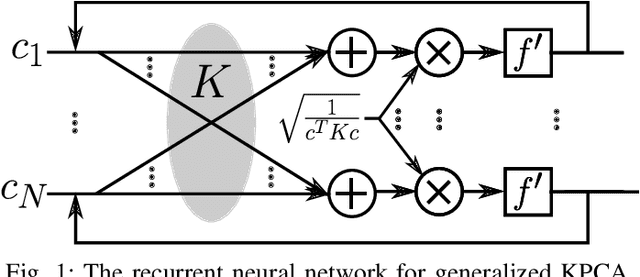
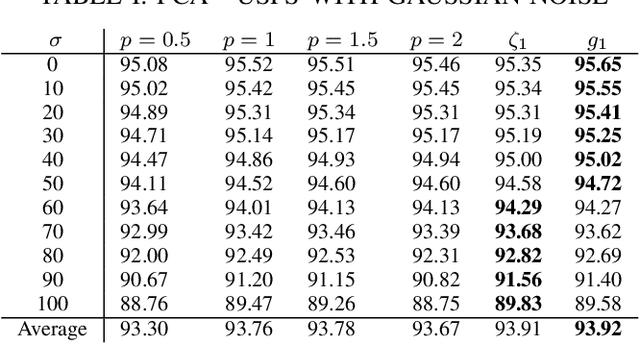

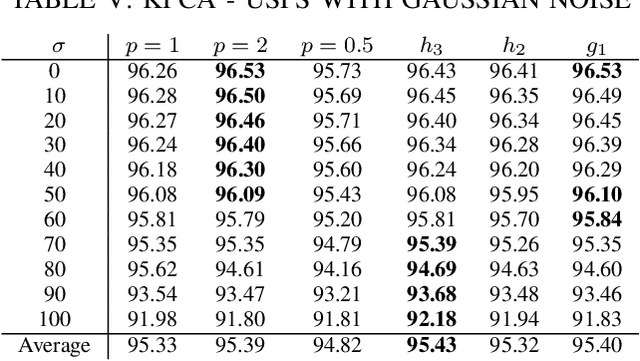




Abstract:Conventional principal component analysis (PCA) finds a principal vector that maximizes the sum of second powers of principal components. We consider a generalized PCA that aims at maximizing the sum of an arbitrary convex function of principal components. We present a gradient ascent algorithm to solve the problem. For the kernel version of generalized PCA, we show that the solutions can be obtained as fixed points of a simple single-layer recurrent neural network. We also evaluate our algorithms on different datasets.
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge