From Glucose Patterns to Health Outcomes: A Generalizable Foundation Model for Continuous Glucose Monitor Data Analysis

Recent advances in self-supervised learning enabled novel medical AI models, known as foundation models (FMs) that offer great potential for characterizing health from diverse biomedical data. Continuous glucose monitoring (CGM) provides rich, temporal data on glycemic patterns, but its full potential for predicting broader health outcomes remains underutilized. Here, we present GluFormer, a generative foundation model on biomedical temporal data based on a transformer architecture, and trained on over 10 million CGM measurements from 10,812 non-diabetic individuals. We tokenized the CGM training data and trained GluFormer using next token prediction in a generative, autoregressive manner. We demonstrate that GluFormer generalizes effectively to 15 different external datasets, including 4936 individuals across 5 different geographical regions, 6 different CGM devices, and several metabolic disorders, including normoglycemic, prediabetic, and diabetic populations, as well as those with gestational diabetes and obesity. GluFormer produces embeddings which outperform traditional CGM analysis tools, and achieves high Pearson correlations in predicting clinical parameters such as HbA1c, liver-related parameters, blood lipids, and sleep-related indices. Notably, GluFormer can also predict onset of future health outcomes even 4 years in advance. We also show that CGM embeddings from pre-intervention periods in Randomized Clinical Trials (RCTs) outperform other methods in predicting primary and secondary outcomes. When integrating dietary data into GluFormer, we show that the enhanced model can accurately generate CGM data based only on dietary intake data, simulate outcomes of dietary interventions, and predict individual responses to specific foods. Overall, we show that GluFormer accurately predicts health outcomes which generalize across different populations metabolic conditions.

Efficient Subgraph GNNs by Learning Effective Selection Policies

Subgraph GNNs are provably expressive neural architectures that learn graph representations from sets of subgraphs. Unfortunately, their applicability is hampered by the computational complexity associated with performing message passing on many subgraphs. In this paper, we consider the problem of learning to select a small subset of the large set of possible subgraphs in a data-driven fashion. We first motivate the problem by proving that there are families of WL-indistinguishable graphs for which there exist efficient subgraph selection policies: small subsets of subgraphs that can already identify all the graphs within the family. We then propose a new approach, called Policy-Learn, that learns how to select subgraphs in an iterative manner. We prove that, unlike popular random policies and prior work addressing the same problem, our architecture is able to learn the efficient policies mentioned above. Our experimental results demonstrate that Policy-Learn outperforms existing baselines across a wide range of datasets.

Train Hard, Fight Easy: Robust Meta Reinforcement Learning

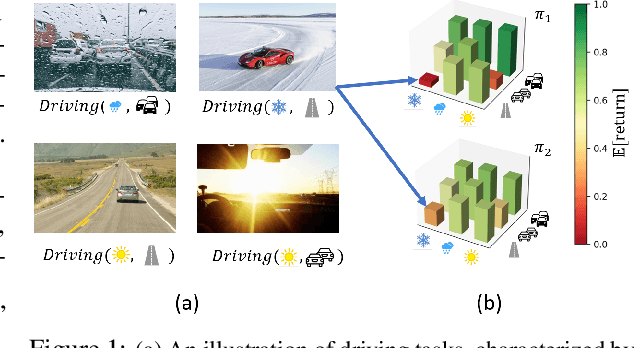
A major challenge of reinforcement learning (RL) in real-world applications is the variation between environments, tasks or clients. Meta-RL (MRL) addresses this issue by learning a meta-policy that adapts to new tasks. Standard MRL methods optimize the average return over tasks, but often suffer from poor results in tasks of high risk or difficulty. This limits system reliability whenever test tasks are not known in advance. In this work, we propose a robust MRL objective with a controlled robustness level. Optimization of analogous robust objectives in RL often leads to both biased gradients and data inefficiency. We prove that the former disappears in MRL, and address the latter via the novel Robust Meta RL algorithm (RoML). RoML is a meta-algorithm that generates a robust version of any given MRL algorithm, by identifying and over-sampling harder tasks throughout training. We demonstrate that RoML learns substantially different meta-policies and achieves robust returns on several navigation and continuous control benchmarks.

On Size Generalization in Graph Neural Networks

Graph neural networks (GNNs) can process graphs of different sizes but their capacity to generalize across sizes is still not well understood. Size generalization is key to numerous GNN applications, from solving combinatorial optimization problems to learning in molecular biology. In such problems, obtaining labels and training on large graphs can be prohibitively expensive, but training on smaller graphs is possible. This paper puts forward the size-generalization question and characterizes important aspects of that problem theoretically and empirically. We show that even for very simple tasks, GNNs do not naturally generalize to graphs of larger size. Instead, their generalization performance is closely related to the distribution of patterns of connectivity and features and how that distribution changes from small to large graphs. Specifically, we show that in many cases, there are GNNs that can perfectly solve a task on small graphs but generalize poorly to large graphs and that these GNNs are encountered in practice. We then formalize size generalization as a domain-adaption problem and describe two learning setups where size generalization can be improved. First, as a self-supervised learning problem (SSL) over the target domain of large graphs. Second, as a semi-supervised learning problem when few samples are available in the target domain. We demonstrate the efficacy of these solutions on a diverse set of benchmark graph datasets.