Training neural operators to preserve invariant measures of chaotic attractors

Chaotic systems make long-horizon forecasts difficult because small perturbations in initial conditions cause trajectories to diverge at an exponential rate. In this setting, neural operators trained to minimize squared error losses, while capable of accurate short-term forecasts, often fail to reproduce statistical or structural properties of the dynamics over longer time horizons and can yield degenerate results. In this paper, we propose an alternative framework designed to preserve invariant measures of chaotic attractors that characterize the time-invariant statistical properties of the dynamics. Specifically, in the multi-environment setting (where each sample trajectory is governed by slightly different dynamics), we consider two novel approaches to training with noisy data. First, we propose a loss based on the optimal transport distance between the observed dynamics and the neural operator outputs. This approach requires expert knowledge of the underlying physics to determine what statistical features should be included in the optimal transport loss. Second, we show that a contrastive learning framework, which does not require any specialized prior knowledge, can preserve statistical properties of the dynamics nearly as well as the optimal transport approach. On a variety of chaotic systems, our method is shown empirically to preserve invariant measures of chaotic attractors.

Deep Stochastic Mechanics

This paper introduces a novel deep-learning-based approach for numerical simulation of a time-evolving Schr\"odinger equation inspired by stochastic mechanics and generative diffusion models. Unlike existing approaches, which exhibit computational complexity that scales exponentially in the problem dimension, our method allows us to adapt to the latent low-dimensional structure of the wave function by sampling from the Markovian diffusion. Depending on the latent dimension, our method may have far lower computational complexity in higher dimensions. Moreover, we propose novel equations for stochastic quantum mechanics, resulting in linear computational complexity with respect to the number of dimensions. Numerical simulations verify our theoretical findings and show a significant advantage of our method compared to other deep-learning-based approaches used for quantum mechanics.

Beyond Ensemble Averages: Leveraging Climate Model Ensembles for Subseasonal Forecasting

Producing high-quality forecasts of key climate variables such as temperature and precipitation on subseasonal time scales has long been a gap in operational forecasting. Recent studies have shown promising results using machine learning (ML) models to advance subseasonal forecasting (SSF), but several open questions remain. First, several past approaches use the average of an ensemble of physics-based forecasts as an input feature of these models. However, ensemble forecasts contain information that can aid prediction beyond only the ensemble mean. Second, past methods have focused on average performance, whereas forecasts of extreme events are far more important for planning and mitigation purposes. Third, climate forecasts correspond to a spatially-varying collection of forecasts, and different methods account for spatial variability in the response differently. Trade-offs between different approaches may be mitigated with model stacking. This paper describes the application of a variety of ML methods used to predict monthly average precipitation and two meter temperature using physics-based predictions (ensemble forecasts) and observational data such as relative humidity, pressure at sea level, or geopotential height, two weeks in advance for the whole continental United States. Regression, quantile regression, and tercile classification tasks using linear models, random forests, convolutional neural networks, and stacked models are considered. The proposed models outperform common baselines such as historical averages (or quantiles) and ensemble averages (or quantiles). This paper further includes an investigation of feature importance, trade-offs between using the full ensemble or only the ensemble average, and different modes of accounting for spatial variability.

Comparing the costs of abstraction for DL frameworks

High level abstractions for implementing, training, and testing Deep Learning (DL) models abound. Such frameworks function primarily by abstracting away the implementation details of arbitrary neural architectures, thereby enabling researchers and engineers to focus on design. In principle, such frameworks could be "zero-cost abstractions"; in practice, they incur translation and indirection overheads. We study at which points exactly in the engineering life-cycle of a DL model the highest costs are paid and whether they can be mitigated. We train, test, and evaluate a representative DL model using PyTorch, LibTorch, TorchScript, and cuDNN on representative datasets, comparing accuracy, execution time and memory efficiency.

Generative Models for Fast Calorimeter Simulation.LHCb case

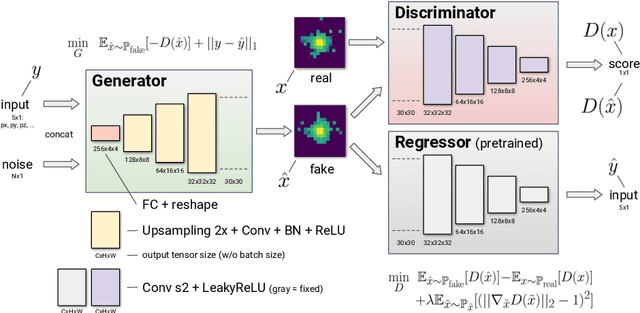
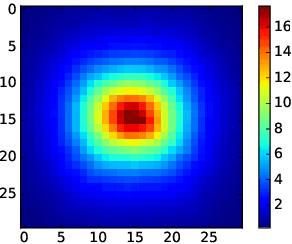
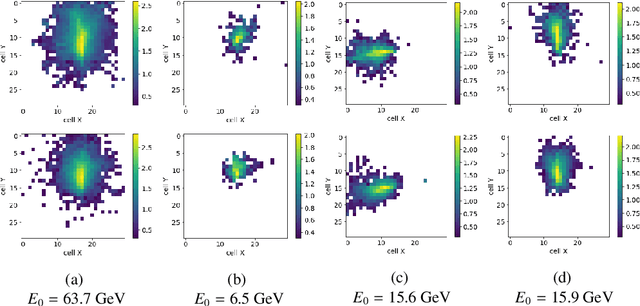
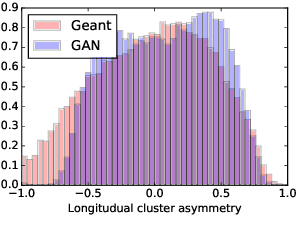
Simulation is one of the key components in high energy physics. Historically it relies on the Monte Carlo methods which require a tremendous amount of computation resources. These methods may have difficulties with the expected High Luminosity Large Hadron Collider (HL LHC) need, so the experiment is in urgent need of new fast simulation techniques. We introduce a new Deep Learning framework based on Generative Adversarial Networks which can be faster than traditional simulation methods by 5 order of magnitude with reasonable simulation accuracy. This approach will allow physicists to produce a big enough amount of simulated data needed by the next HL LHC experiments using limited computing resources.