Classifier Weighted Mixture models

This paper proposes an extension of standard mixture stochastic models, by replacing the constant mixture weights with functional weights defined using a classifier. Classifier Weighted Mixtures enable straightforward density evaluation, explicit sampling, and enhanced expressivity in variational estimation problems, without increasing the number of components nor the complexity of the mixture components.

Targeting the partition function of chemically disordered materials with a generative approach based on inverse variational autoencoders

Computing atomic-scale properties of chemically disordered materials requires an efficient exploration of their vast configuration space. Traditional approaches such as Monte Carlo or Special Quasirandom Structures either entail sampling an excessive amount of configurations or do not ensure that the configuration space has been properly covered. In this work, we propose a novel approach where generative machine learning is used to yield a representative set of configurations for accurate property evaluation and provide accurate estimations of atomic-scale properties with minimal computational cost. Our method employs a specific type of variational autoencoder with inverse roles for the encoder and decoder, enabling the application of an unsupervised active learning scheme that does not require any initial training database. The model iteratively generates configuration batches, whose properties are computed with conventional atomic-scale methods. These results are then fed back into the model to estimate the partition function, repeating the process until convergence. We illustrate our approach by computing point-defect formation energies and concentrations in (U, Pu)O2 mixed-oxide fuels. In addition, the ML model provides valuable insights into the physical factors influencing the target property. Our method is generally applicable to explore other properties, such as atomic-scale diffusion coefficients, in ideally or non-ideally disordered materials like high-entropy alloys.

Targetin the partition function of chemically disordered materials with a generative approach based on inverse variational autoencoders

Computing atomic-scale properties of chemically disordered materials requires an efficient exploration of their vast configuration space. Traditional approaches such as Monte Carlo or Special Quasirandom Structures either entail sampling an excessive amount of configurations or do not ensure that the configuration space has been properly covered. In this work, we propose a novel approach where generative machine learning is used to yield a representative set of configurations for accurate property evaluation and provide accurate estimations of atomic-scale properties with minimal computational cost. Our method employs a specific type of variational autoencoder with inverse roles for the encoder and decoder, enabling the application of an unsupervised active learning scheme that does not require any initial training database. The model iteratively generates configuration batches, whose properties are computed with conventional atomic-scale methods. These results are then fed back into the model to estimate the partition function, repeating the process until convergence. We illustrate our approach by computing point-defect formation energies and concentrations in (U, Pu)O2 mixed-oxide fuels. In addition, the ML model provides valuable insights into the physical factors influencing the target property. Our method is generally applicable to explore other properties, such as atomic-scale diffusion coefficients, in ideally or non-ideally disordered materials like high-entropy alloys.

Generative vs. Discriminative modeling under the lens of uncertainty quantification

Learning a parametric model from a given dataset indeed enables to capture intrinsic dependencies between random variables via a parametric conditional probability distribution and in turn predict the value of a label variable given observed variables. In this paper, we undertake a comparative analysis of generative and discriminative approaches which differ in their construction and the structure of the underlying inference problem. Our objective is to compare the ability of both approaches to leverage information from various sources in an epistemic uncertainty aware inference via the posterior predictive distribution. We assess the role of a prior distribution, explicit in the generative case and implicit in the discriminative case, leading to a discussion about discriminative models suffering from imbalanced dataset. We next examine the double role played by the observed variables in the generative case, and discuss the compatibility of both approaches with semi-supervised learning. We also provide with practical insights and we examine how the modeling choice impacts the sampling from the posterior predictive distribution. With regard to this, we propose a general sampling scheme enabling supervised learning for both approaches, as well as semi-supervised learning when compatible with the considered modeling approach. Throughout this paper, we illustrate our arguments and conclusions using the example of affine regression, and validate our comparative analysis through classification simulations using neural network based models.

Multivariate Bayesian Last Layer for Regression: Uncertainty Quantification and Disentanglement

We present new Bayesian Last Layer models in the setting of multivariate regression under heteroscedastic noise, and propose an optimization algorithm for parameter learning. Bayesian Last Layer combines Bayesian modelling of the predictive distribution with neural networks for parameterization of the prior, and has the attractive property of uncertainty quantification with a single forward pass. The proposed framework is capable of disentangling the aleatoric and epistemic uncertainty, and can be used to transfer a canonically trained deep neural network to new data domains with uncertainty-aware capability.

Data Subsampling for Bayesian Neural Networks

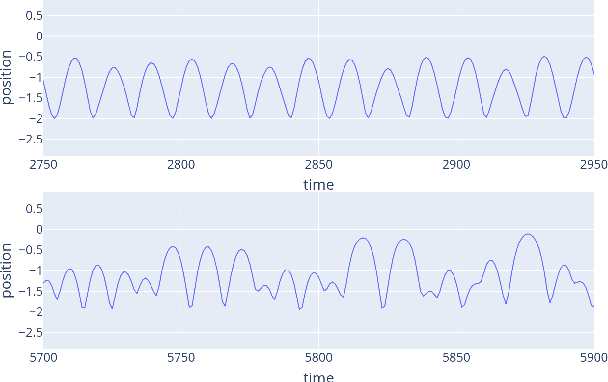
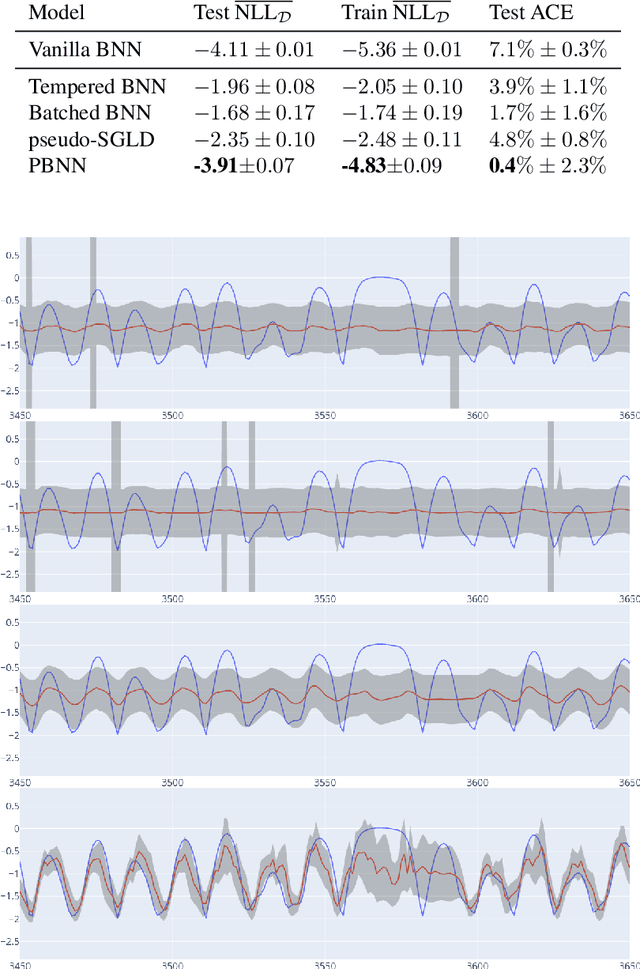
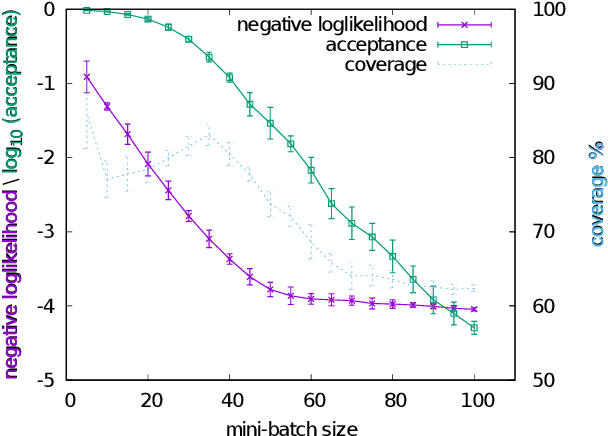
Markov Chain Monte Carlo (MCMC) algorithms do not scale well for large datasets leading to difficulties in Neural Network posterior sampling. In this paper, we apply a generalization of the Metropolis Hastings algorithm that allows us to restrict the evaluation of the likelihood to small mini-batches in a Bayesian inference context. Since it requires the computation of a so-called "noise penalty" determined by the variance of the training loss function over the mini-batches, we refer to this data subsampling strategy as Penalty Bayesian Neural Networks - PBNNs. Its implementation on top of MCMC is straightforward, as the variance of the loss function merely reduces the acceptance probability. Comparing to other samplers, we empirically show that PBNN achieves good predictive performance for a given mini-batch size. Varying the size of the mini-batches enables a natural calibration of the predictive distribution and provides an inbuilt protection against overfitting. We expect PBNN to be particularly suited for cases when data sets are distributed across multiple decentralized devices as typical in federated learning.

Discretely Indexed Flows

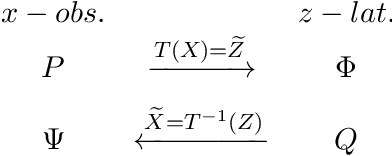
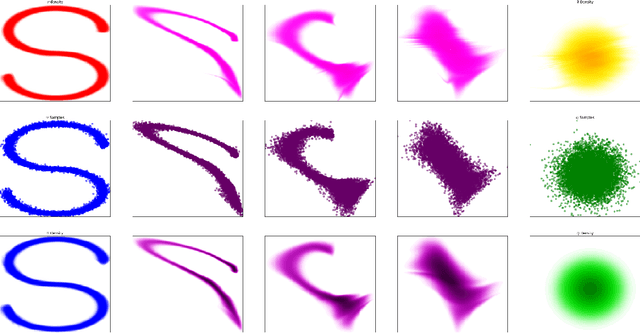
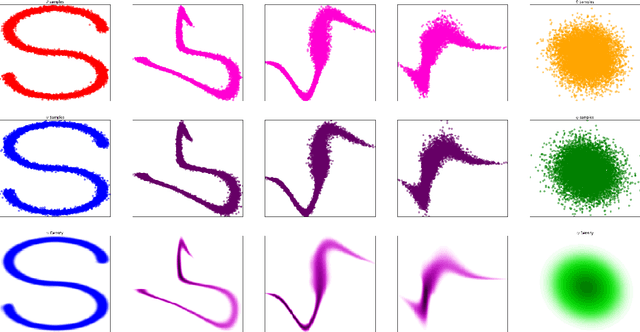
In this paper we propose Discretely Indexed flows (DIF) as a new tool for solving variational estimation problems. Roughly speaking, DIF are built as an extension of Normalizing Flows (NF), in which the deterministic transport becomes stochastic, and more precisely discretely indexed. Due to the discrete nature of the underlying additional latent variable, DIF inherit the good computational behavior of NF: they benefit from both a tractable density as well as a straightforward sampling scheme, and can thus be used for the dual problems of Variational Inference (VI) and of Variational density estimation (VDE). On the other hand, DIF can also be understood as an extension of mixture density models, in which the constant mixture weights are replaced by flexible functions. As a consequence, DIF are better suited for capturing distributions with discontinuities, sharp edges and fine details, which is a main advantage of this construction. Finally we propose a methodology for constructiong DIF in practice, and see that DIF can be sequentially cascaded, and cascaded with NF.