Bregman geometry-aware split Gibbs sampling for Bayesian Poisson inverse problems

This paper proposes a novel Bayesian framework for solving Poisson inverse problems by devising a Monte Carlo sampling algorithm which accounts for the underlying non-Euclidean geometry. To address the challenges posed by the Poisson likelihood -- such as non-Lipschitz gradients and positivity constraints -- we derive a Bayesian model which leverages exact and asymptotically exact data augmentations. In particular, the augmented model incorporates two sets of splitting variables both derived through a Bregman divergence based on the Burg entropy. Interestingly the resulting augmented posterior distribution is characterized by conditional distributions which benefit from natural conjugacy properties and preserve the intrinsic geometry of the latent and splitting variables. This allows for efficient sampling via Gibbs steps, which can be performed explicitly for all conditionals, except the one incorporating the regularization potential. For this latter, we resort to a Hessian Riemannian Langevin Monte Carlo (HRLMC) algorithm which is well suited to handle priors with explicit or easily computable score functions. By operating on a mirror manifold, this Langevin step ensures that the sampling satisfies the positivity constraints and more accurately reflects the underlying problem structure. Performance results obtained on denoising, deblurring, and positron emission tomography (PET) experiments demonstrate that the method achieves competitive performance in terms of reconstruction quality compared to optimization- and sampling-based approaches.

Classifier Weighted Mixture models

This paper proposes an extension of standard mixture stochastic models, by replacing the constant mixture weights with functional weights defined using a classifier. Classifier Weighted Mixtures enable straightforward density evaluation, explicit sampling, and enhanced expressivity in variational estimation problems, without increasing the number of components nor the complexity of the mixture components.

Generative vs. Discriminative modeling under the lens of uncertainty quantification

Learning a parametric model from a given dataset indeed enables to capture intrinsic dependencies between random variables via a parametric conditional probability distribution and in turn predict the value of a label variable given observed variables. In this paper, we undertake a comparative analysis of generative and discriminative approaches which differ in their construction and the structure of the underlying inference problem. Our objective is to compare the ability of both approaches to leverage information from various sources in an epistemic uncertainty aware inference via the posterior predictive distribution. We assess the role of a prior distribution, explicit in the generative case and implicit in the discriminative case, leading to a discussion about discriminative models suffering from imbalanced dataset. We next examine the double role played by the observed variables in the generative case, and discuss the compatibility of both approaches with semi-supervised learning. We also provide with practical insights and we examine how the modeling choice impacts the sampling from the posterior predictive distribution. With regard to this, we propose a general sampling scheme enabling supervised learning for both approaches, as well as semi-supervised learning when compatible with the considered modeling approach. Throughout this paper, we illustrate our arguments and conclusions using the example of affine regression, and validate our comparative analysis through classification simulations using neural network based models.

Discretely Indexed Flows

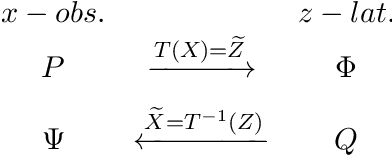
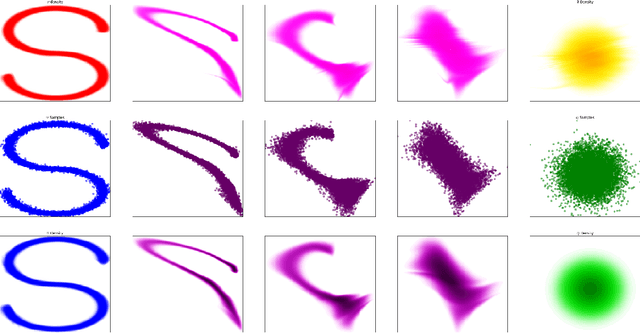
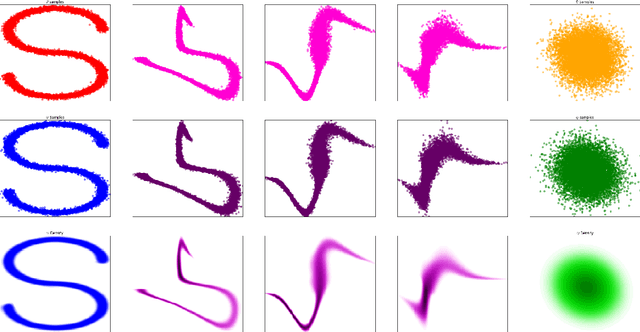
In this paper we propose Discretely Indexed flows (DIF) as a new tool for solving variational estimation problems. Roughly speaking, DIF are built as an extension of Normalizing Flows (NF), in which the deterministic transport becomes stochastic, and more precisely discretely indexed. Due to the discrete nature of the underlying additional latent variable, DIF inherit the good computational behavior of NF: they benefit from both a tractable density as well as a straightforward sampling scheme, and can thus be used for the dual problems of Variational Inference (VI) and of Variational density estimation (VDE). On the other hand, DIF can also be understood as an extension of mixture density models, in which the constant mixture weights are replaced by flexible functions. As a consequence, DIF are better suited for capturing distributions with discontinuities, sharp edges and fine details, which is a main advantage of this construction. Finally we propose a methodology for constructiong DIF in practice, and see that DIF can be sequentially cascaded, and cascaded with NF.