Generative vs. Discriminative modeling under the lens of uncertainty quantification

Learning a parametric model from a given dataset indeed enables to capture intrinsic dependencies between random variables via a parametric conditional probability distribution and in turn predict the value of a label variable given observed variables. In this paper, we undertake a comparative analysis of generative and discriminative approaches which differ in their construction and the structure of the underlying inference problem. Our objective is to compare the ability of both approaches to leverage information from various sources in an epistemic uncertainty aware inference via the posterior predictive distribution. We assess the role of a prior distribution, explicit in the generative case and implicit in the discriminative case, leading to a discussion about discriminative models suffering from imbalanced dataset. We next examine the double role played by the observed variables in the generative case, and discuss the compatibility of both approaches with semi-supervised learning. We also provide with practical insights and we examine how the modeling choice impacts the sampling from the posterior predictive distribution. With regard to this, we propose a general sampling scheme enabling supervised learning for both approaches, as well as semi-supervised learning when compatible with the considered modeling approach. Throughout this paper, we illustrate our arguments and conclusions using the example of affine regression, and validate our comparative analysis through classification simulations using neural network based models.

Neural Classifiers based Monte Carlo simulation

Acceptance-rejection (AR), Independent Metropolis Hastings (IMH) or importance sampling (IS) Monte Carlo (MC) simulation algorithms all involve computing ratios of probability density functions (pdfs). On the other hand, classifiers discriminate labellized samples produced by a mixture density model, i.e., a convex linear combination of two pdfs, and can thus be used for approximating the ratio of these two densities. This bridge between simulation and classification techniques enables us to propose (approximate) pdf-ratios-based simulation algorithms which are built only from a labellized training data set.

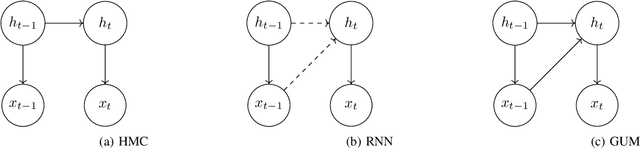
Expressivity of Hidden Markov Chains vs. Recurrent Neural Networks from a system theoretic viewpoint

Hidden Markov Chains (HMC) and Recurrent Neural Networks (RNN) are two well known tools for predicting time series. Even though these solutions were developed independently in distinct communities, they share some similarities when considered as probabilistic structures. So in this paper we first consider HMC and RNN as generative models, and we embed both structures in a common generative unified model (GUM). We next address a comparative study of the expressivity of these models. To that end we assume that the models are furthermore linear and Gaussian. The probability distributions produced by these models are characterized by structured covariance series, and as a consequence expressivity reduces to comparing sets of structured covariance series, which enables us to call for stochastic realization theory (SRT). We finally provide conditions under which a given covariance series can be realized by a GUM, an HMC or an RNN.

Discretely Indexed Flows

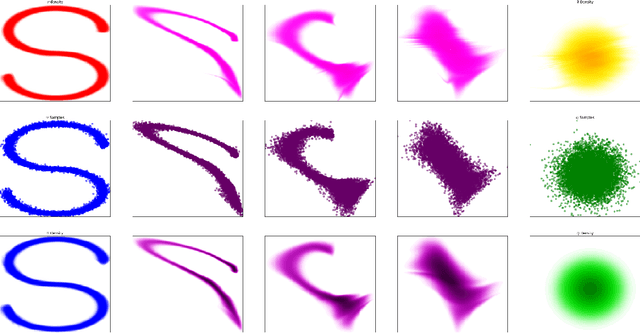
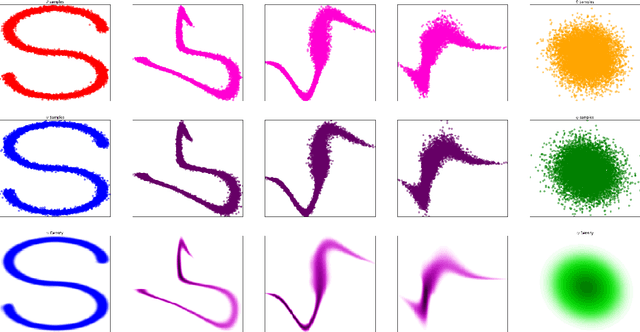
In this paper we propose Discretely Indexed flows (DIF) as a new tool for solving variational estimation problems. Roughly speaking, DIF are built as an extension of Normalizing Flows (NF), in which the deterministic transport becomes stochastic, and more precisely discretely indexed. Due to the discrete nature of the underlying additional latent variable, DIF inherit the good computational behavior of NF: they benefit from both a tractable density as well as a straightforward sampling scheme, and can thus be used for the dual problems of Variational Inference (VI) and of Variational density estimation (VDE). On the other hand, DIF can also be understood as an extension of mixture density models, in which the constant mixture weights are replaced by flexible functions. As a consequence, DIF are better suited for capturing distributions with discontinuities, sharp edges and fine details, which is a main advantage of this construction. Finally we propose a methodology for constructiong DIF in practice, and see that DIF can be sequentially cascaded, and cascaded with NF.