Discretely Indexed Flows
Paper and Code
Apr 04, 2022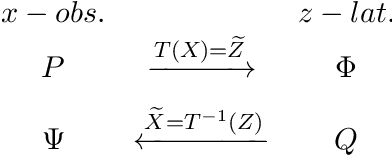
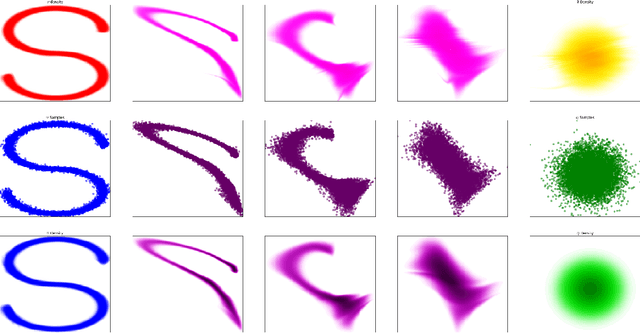
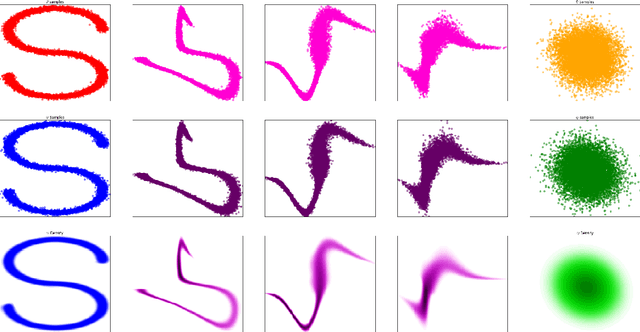

In this paper we propose Discretely Indexed flows (DIF) as a new tool for solving variational estimation problems. Roughly speaking, DIF are built as an extension of Normalizing Flows (NF), in which the deterministic transport becomes stochastic, and more precisely discretely indexed. Due to the discrete nature of the underlying additional latent variable, DIF inherit the good computational behavior of NF: they benefit from both a tractable density as well as a straightforward sampling scheme, and can thus be used for the dual problems of Variational Inference (VI) and of Variational density estimation (VDE). On the other hand, DIF can also be understood as an extension of mixture density models, in which the constant mixture weights are replaced by flexible functions. As a consequence, DIF are better suited for capturing distributions with discontinuities, sharp edges and fine details, which is a main advantage of this construction. Finally we propose a methodology for constructiong DIF in practice, and see that DIF can be sequentially cascaded, and cascaded with NF.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge