Discretely Indexed Flows

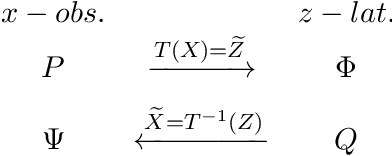
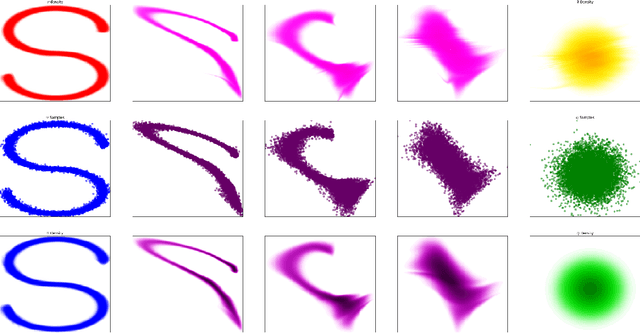
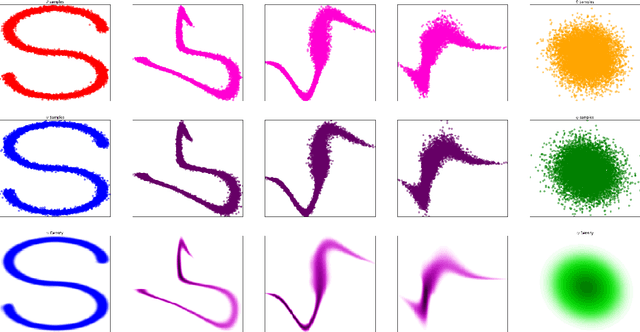
In this paper we propose Discretely Indexed flows (DIF) as a new tool for solving variational estimation problems. Roughly speaking, DIF are built as an extension of Normalizing Flows (NF), in which the deterministic transport becomes stochastic, and more precisely discretely indexed. Due to the discrete nature of the underlying additional latent variable, DIF inherit the good computational behavior of NF: they benefit from both a tractable density as well as a straightforward sampling scheme, and can thus be used for the dual problems of Variational Inference (VI) and of Variational density estimation (VDE). On the other hand, DIF can also be understood as an extension of mixture density models, in which the constant mixture weights are replaced by flexible functions. As a consequence, DIF are better suited for capturing distributions with discontinuities, sharp edges and fine details, which is a main advantage of this construction. Finally we propose a methodology for constructiong DIF in practice, and see that DIF can be sequentially cascaded, and cascaded with NF.

Nonparametric posterior learning for emission tomography with multimodal data

In this work we continue studies of the uncertainty quantification problem in emission tomographies such as PET or SPECT. In particular, we consider a scenario when additional multimodal data (e.g., anatomical MRI images) are available. To solve the aforementioned problem we adapt the recently proposed nonparametric posterior learning technique to the context of Poisson-type data in emission tomography. Using this approach we derive sampling algorithms which are trivially parallelizable, scalable and very easy to implement. In addition, we prove conditional consistency and tightness for the distribution of produced samples in the small noise limit (i.e., when the acquisition time tends to infinity) and derive new geometrical and necessary condition on how MRI images must be used. This condition arises naturally in the context of misspecified generalized Poisson models. We also contrast our approach with bayesian MCMC sampling based one one data augmentation scheme which is very popular in the context of EM-type algorithms for PET or SPECT. We show theoretically and also numerically that such data augmentation significantly increases mixing times for the Markov chain. In view of this, our algorithms seem to give a reasonable trade-off between design complexity, scalability, numerical load and asessement for the uncertainty quantification.