Expressivity of Hidden Markov Chains vs. Recurrent Neural Networks from a system theoretic viewpoint
Paper and Code
Aug 17, 2022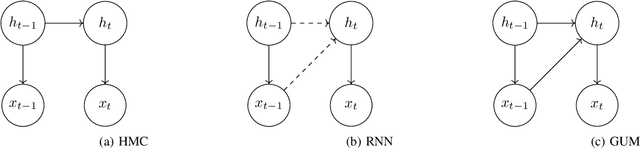

Hidden Markov Chains (HMC) and Recurrent Neural Networks (RNN) are two well known tools for predicting time series. Even though these solutions were developed independently in distinct communities, they share some similarities when considered as probabilistic structures. So in this paper we first consider HMC and RNN as generative models, and we embed both structures in a common generative unified model (GUM). We next address a comparative study of the expressivity of these models. To that end we assume that the models are furthermore linear and Gaussian. The probability distributions produced by these models are characterized by structured covariance series, and as a consequence expressivity reduces to comparing sets of structured covariance series, which enables us to call for stochastic realization theory (SRT). We finally provide conditions under which a given covariance series can be realized by a GUM, an HMC or an RNN.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge