Data Subsampling for Bayesian Neural Networks
Paper and Code
Oct 17, 2022
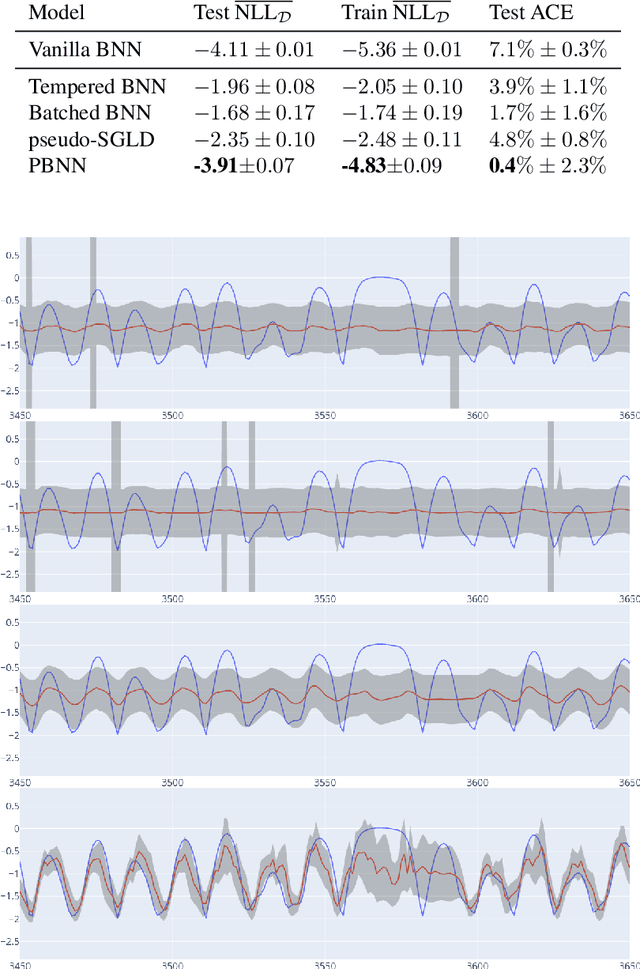
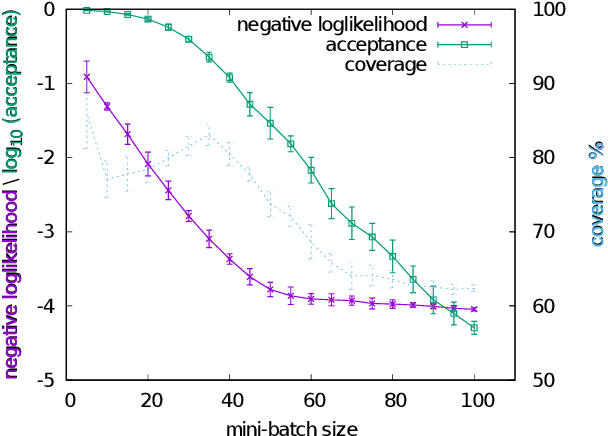
Markov Chain Monte Carlo (MCMC) algorithms do not scale well for large datasets leading to difficulties in Neural Network posterior sampling. In this paper, we apply a generalization of the Metropolis Hastings algorithm that allows us to restrict the evaluation of the likelihood to small mini-batches in a Bayesian inference context. Since it requires the computation of a so-called "noise penalty" determined by the variance of the training loss function over the mini-batches, we refer to this data subsampling strategy as Penalty Bayesian Neural Networks - PBNNs. Its implementation on top of MCMC is straightforward, as the variance of the loss function merely reduces the acceptance probability. Comparing to other samplers, we empirically show that PBNN achieves good predictive performance for a given mini-batch size. Varying the size of the mini-batches enables a natural calibration of the predictive distribution and provides an inbuilt protection against overfitting. We expect PBNN to be particularly suited for cases when data sets are distributed across multiple decentralized devices as typical in federated learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge