A GPU-Accelerated Bi-linear ADMM Algorithm for Distributed Sparse Machine Learning

This paper introduces the Bi-linear consensus Alternating Direction Method of Multipliers (Bi-cADMM), aimed at solving large-scale regularized Sparse Machine Learning (SML) problems defined over a network of computational nodes. Mathematically, these are stated as minimization problems with convex local loss functions over a global decision vector, subject to an explicit $\ell_0$ norm constraint to enforce the desired sparsity. The considered SML problem generalizes different sparse regression and classification models, such as sparse linear and logistic regression, sparse softmax regression, and sparse support vector machines. Bi-cADMM leverages a bi-linear consensus reformulation of the original non-convex SML problem and a hierarchical decomposition strategy that divides the problem into smaller sub-problems amenable to parallel computing. In Bi-cADMM, this decomposition strategy is based on a two-phase approach. Initially, it performs a sample decomposition of the data and distributes local datasets across computational nodes. Subsequently, a delayed feature decomposition of the data is conducted on Graphics Processing Units (GPUs) available to each node. This methodology allows Bi-cADMM to undertake computationally intensive data-centric computations on GPUs, while CPUs handle more cost-effective computations. The proposed algorithm is implemented within an open-source Python package called Parallel Sparse Fitting Toolbox (PsFiT), which is publicly available. Finally, computational experiments demonstrate the efficiency and scalability of our algorithm through numerical benchmarks across various SML problems featuring distributed datasets.

Physics-Informed Neural Networks with Skip Connections for Modeling and Control of Gas-Lifted Oil Wells

Neural networks, while powerful, often lack interpretability. Physics-Informed Neural Networks (PINNs) address this limitation by incorporating physics laws into the loss function, making them applicable to solving Ordinary Differential Equations (ODEs) and Partial Differential Equations (PDEs). The recently introduced PINC framework extends PINNs to control applications, allowing for open-ended long-range prediction and control of dynamic systems. In this work, we enhance PINC for modeling highly nonlinear systems such as gas-lifted oil wells. By introducing skip connections in the PINC network and refining certain terms in the ODE, we achieve more accurate gradients during training, resulting in an effective modeling process for the oil well system. Our proposed improved PINC demonstrates superior performance, reducing the validation prediction error by an average of 67% in the oil well application and significantly enhancing gradient flow through the network layers, increasing its magnitude by four orders of magnitude compared to the original PINC. Furthermore, experiments showcase the efficacy of Model Predictive Control (MPC) in regulating the bottom-hole pressure of the oil well using the improved PINC model, even in the presence of noisy measurements.

Deep-learning-based Early Fixing for Gas-lifted Oil Production Optimization: Supervised and Weakly-supervised Approaches

Maximizing oil production from gas-lifted oil wells entails solving Mixed-Integer Linear Programs (MILPs). As the parameters of the wells, such as the basic-sediment-to-water ratio and the gas-oil ratio, are updated, the problems must be repeatedly solved. Instead of relying on costly exact methods or the accuracy of general approximate methods, in this paper, we propose a tailor-made heuristic solution based on deep learning models trained to provide values to all integer variables given varying well parameters, early-fixing the integer variables and, thus, reducing the original problem to a linear program (LP). We propose two approaches for developing the learning-based heuristic: a supervised learning approach, which requires the optimal integer values for several instances of the original problem in the training set, and a weakly-supervised learning approach, which requires only solutions for the early-fixed linear problems with random assignments for the integer variables. Our results show a runtime reduction of 71.11% Furthermore, the weakly-supervised learning model provided significant values for early fixing, despite never seeing the optimal values during training.

A Graph Neural Network Approach to Nanosatellite Task Scheduling: Insights into Learning Mixed-Integer Models

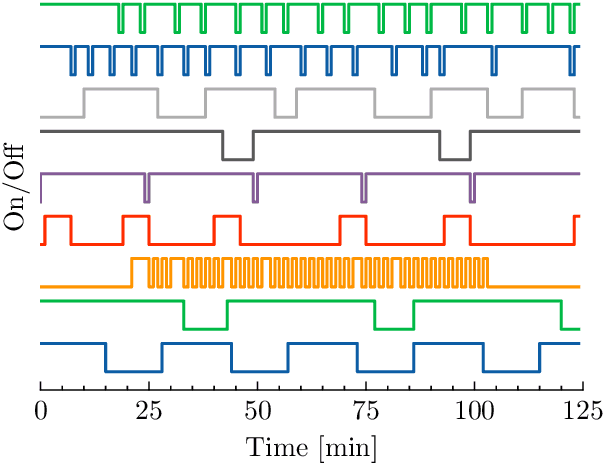
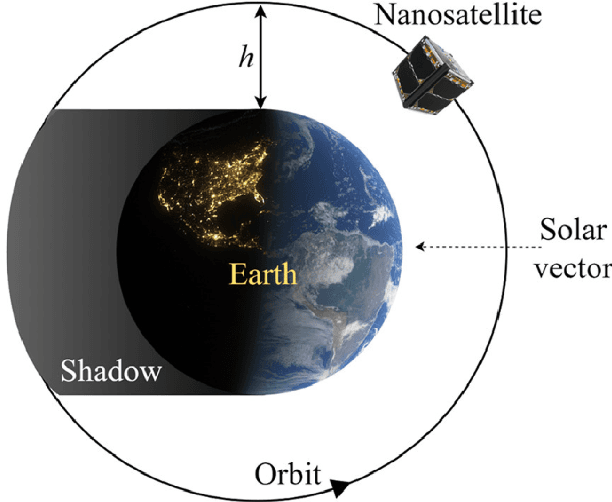
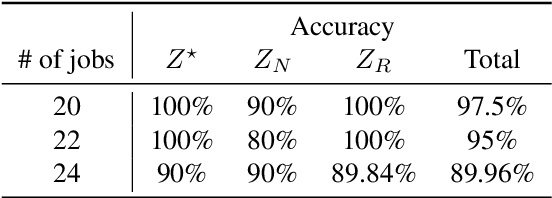
This study investigates how to schedule nanosatellite tasks more efficiently using Graph Neural Networks (GNN). In the Offline Nanosatellite Task Scheduling (ONTS) problem, the goal is to find the optimal schedule for tasks to be carried out in orbit while taking into account Quality-of-Service (QoS) considerations such as priority, minimum and maximum activation events, execution time-frames, periods, and execution windows, as well as constraints on the satellite's power resources and the complexity of energy harvesting and management. The ONTS problem has been approached using conventional mathematical formulations and precise methods, but their applicability to challenging cases of the problem is limited. This study examines the use of GNNs in this context, which has been effectively applied to many optimization problems, including traveling salesman problems, scheduling problems, and facility placement problems. Here, we fully represent MILP instances of the ONTS problem in bipartite graphs. We apply a feature aggregation and message-passing methodology allied to a ReLU activation function to learn using a classic deep learning model, obtaining an optimal set of parameters. Furthermore, we apply Explainable AI (XAI), another emerging field of research, to determine which features -- nodes, constraints -- had the most significant impact on learning performance, shedding light on the inner workings and decision process of such models. We also explored an early fixing approach by obtaining an accuracy above 80\% both in predicting the feasibility of a solution and the probability of a decision variable value being in the optimal solution. Our results point to GNNs as a potentially effective method for scheduling nanosatellite tasks and shed light on the advantages of explainable machine learning models for challenging combinatorial optimization problems.

Vertex-based reachability analysis for verifying ReLU deep neural networks

Neural networks achieved high performance over different tasks, i.e. image identification, voice recognition and other applications. Despite their success, these models are still vulnerable regarding small perturbations, which can be used to craft the so-called adversarial examples. Different approaches have been proposed to circumvent their vulnerability, including formal verification systems, which employ a variety of techniques, including reachability, optimization and search procedures, to verify that the model satisfies some property. In this paper we propose three novel reachability algorithms for verifying deep neural networks with ReLU activations. The first and third algorithms compute an over-approximation for the reachable set, whereas the second one computes the exact reachable set. Differently from previously proposed approaches, our algorithms take as input a V-polytope. Our experiments on the ACAS Xu problem show that the Exact Polytope Network Mapping (EPNM) reachability algorithm proposed in this work surpass the state-of-the-art results from the literature, specially in relation to other reachability methods.

Investigation of Proper Orthogonal Decomposition for Echo State Networks

Echo State Networks (ESN) are a type of Recurrent Neural Networks that yields promising results in representing time series and nonlinear dynamic systems. Although they are equipped with a very efficient training procedure, Reservoir Computing strategies, such as the ESN, require the use of high order networks, i.e. large number of layers, resulting in number of states that is magnitudes higher than the number of model inputs and outputs. This not only makes the computation of a time step more costly, but also may pose robustness issues when applying ESNs to problems such as Model Predictive Control (MPC) and other optimal control problems. One such way to circumvent this is through Model Order Reduction strategies such as the Proper Orthogonal Decomposition (POD) and its variants (POD-DEIM), whereby we find an equivalent lower order representation to an already trained high dimension ESN. The objective of this work is to investigate and analyze the performance of POD methods in Echo State Networks, evaluating their effectiveness. To this end, we evaluate the Memory Capacity (MC) of the POD-reduced network in comparison to the original (full order) ENS. We also perform experiments on two different numerical case studies: a NARMA10 difference equation and an oil platform containing two wells and one riser. The results show that there is little loss of performance comparing the original ESN to a POD-reduced counterpart, and also that the performance of a POD-reduced ESN tend to be superior to a normal ESN of the same size. Also we attain speedups of around $80\%$ in comparison to the original ESN.

Physics-Informed Neural Nets-based Control

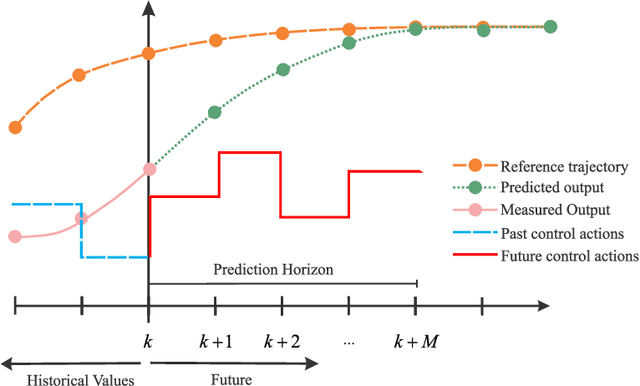
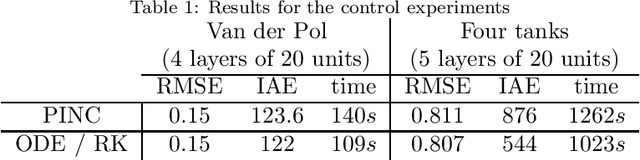
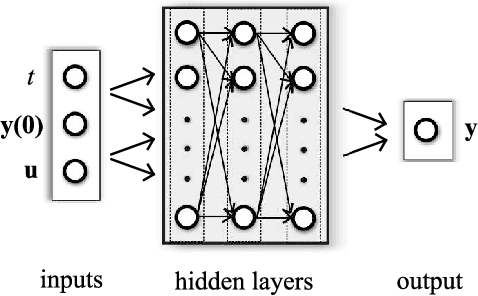
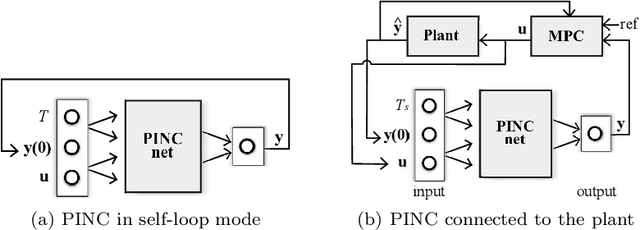
Physics-informed neural networks (PINNs) impose known physical laws into the learning of deep neural networks, making sure they respect the physics of the process while decreasing the demand of labeled data. For systems represented by Ordinary Differential Equations (ODEs), the conventional PINN has a continuous time input variable and outputs the solution of the corresponding ODE. In their original form, PINNs do not allow control inputs neither can they simulate for long-range intervals without serious degradation in their predictions. In this context, this work presents a new framework called Physics-Informed Neural Nets-based Control (PINC), which proposes a novel PINN-based architecture that is amenable to control problems and able to simulate for longer-range time horizons that are not fixed beforehand. First, the network is augmented with new inputs to account for the initial state of the system and the control action. Then, the response over the complete time horizon is split such that each smaller interval constitutes a solution of the ODE conditioned on the fixed values of initial state and control action. The complete response is formed by setting the initial state of the next interval to the terminal state of the previous one. The new methodology enables the optimal control of dynamic systems, making feasible to integrate a priori knowledge from experts and data collected from plants in control applications. We showcase our method in the control of two nonlinear dynamic systems: the Van der Pol oscillator and the four-tank system.