Deep-learning-based Early Fixing for Gas-lifted Oil Production Optimization: Supervised and Weakly-supervised Approaches

Maximizing oil production from gas-lifted oil wells entails solving Mixed-Integer Linear Programs (MILPs). As the parameters of the wells, such as the basic-sediment-to-water ratio and the gas-oil ratio, are updated, the problems must be repeatedly solved. Instead of relying on costly exact methods or the accuracy of general approximate methods, in this paper, we propose a tailor-made heuristic solution based on deep learning models trained to provide values to all integer variables given varying well parameters, early-fixing the integer variables and, thus, reducing the original problem to a linear program (LP). We propose two approaches for developing the learning-based heuristic: a supervised learning approach, which requires the optimal integer values for several instances of the original problem in the training set, and a weakly-supervised learning approach, which requires only solutions for the early-fixed linear problems with random assignments for the integer variables. Our results show a runtime reduction of 71.11% Furthermore, the weakly-supervised learning model provided significant values for early fixing, despite never seeing the optimal values during training.

A Graph Neural Network Approach to Nanosatellite Task Scheduling: Insights into Learning Mixed-Integer Models

This study investigates how to schedule nanosatellite tasks more efficiently using Graph Neural Networks (GNN). In the Offline Nanosatellite Task Scheduling (ONTS) problem, the goal is to find the optimal schedule for tasks to be carried out in orbit while taking into account Quality-of-Service (QoS) considerations such as priority, minimum and maximum activation events, execution time-frames, periods, and execution windows, as well as constraints on the satellite's power resources and the complexity of energy harvesting and management. The ONTS problem has been approached using conventional mathematical formulations and precise methods, but their applicability to challenging cases of the problem is limited. This study examines the use of GNNs in this context, which has been effectively applied to many optimization problems, including traveling salesman problems, scheduling problems, and facility placement problems. Here, we fully represent MILP instances of the ONTS problem in bipartite graphs. We apply a feature aggregation and message-passing methodology allied to a ReLU activation function to learn using a classic deep learning model, obtaining an optimal set of parameters. Furthermore, we apply Explainable AI (XAI), another emerging field of research, to determine which features -- nodes, constraints -- had the most significant impact on learning performance, shedding light on the inner workings and decision process of such models. We also explored an early fixing approach by obtaining an accuracy above 80\% both in predicting the feasibility of a solution and the probability of a decision variable value being in the optimal solution. Our results point to GNNs as a potentially effective method for scheduling nanosatellite tasks and shed light on the advantages of explainable machine learning models for challenging combinatorial optimization problems.

Physics-Informed Neural Nets-based Control

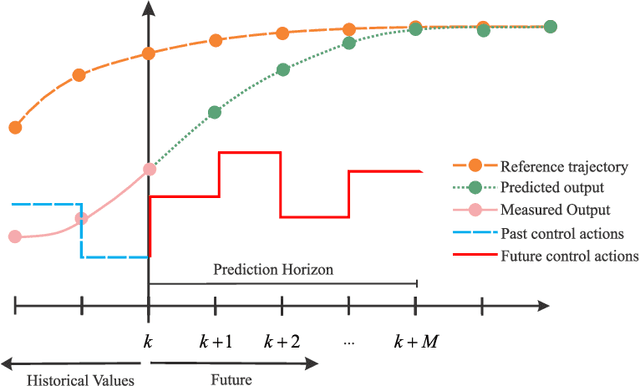
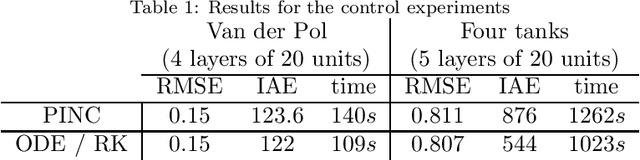
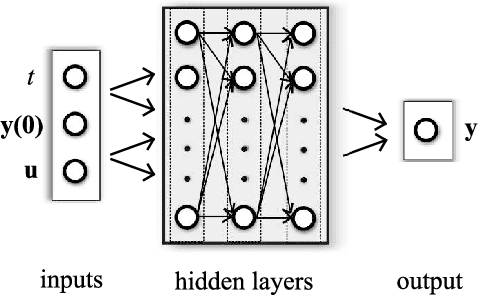
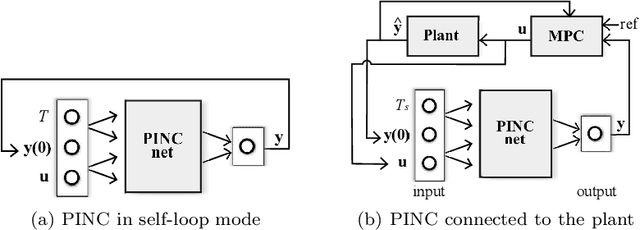
Physics-informed neural networks (PINNs) impose known physical laws into the learning of deep neural networks, making sure they respect the physics of the process while decreasing the demand of labeled data. For systems represented by Ordinary Differential Equations (ODEs), the conventional PINN has a continuous time input variable and outputs the solution of the corresponding ODE. In their original form, PINNs do not allow control inputs neither can they simulate for long-range intervals without serious degradation in their predictions. In this context, this work presents a new framework called Physics-Informed Neural Nets-based Control (PINC), which proposes a novel PINN-based architecture that is amenable to control problems and able to simulate for longer-range time horizons that are not fixed beforehand. First, the network is augmented with new inputs to account for the initial state of the system and the control action. Then, the response over the complete time horizon is split such that each smaller interval constitutes a solution of the ODE conditioned on the fixed values of initial state and control action. The complete response is formed by setting the initial state of the next interval to the terminal state of the previous one. The new methodology enables the optimal control of dynamic systems, making feasible to integrate a priori knowledge from experts and data collected from plants in control applications. We showcase our method in the control of two nonlinear dynamic systems: the Van der Pol oscillator and the four-tank system.