Physics-Informed Neural Nets-based Control
Paper and Code
Apr 06, 2021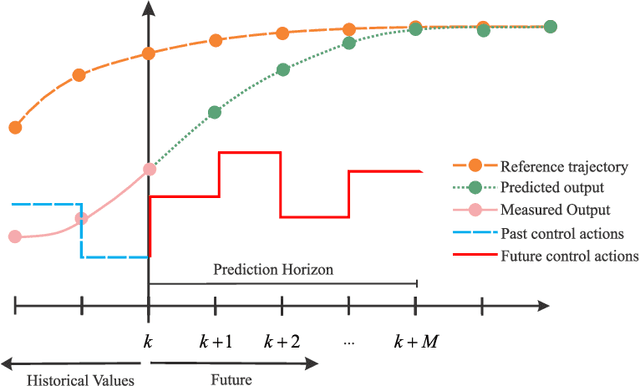
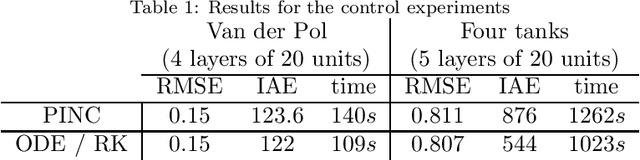
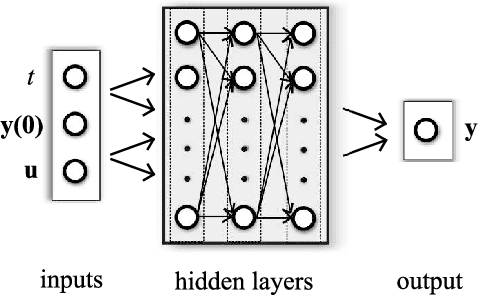
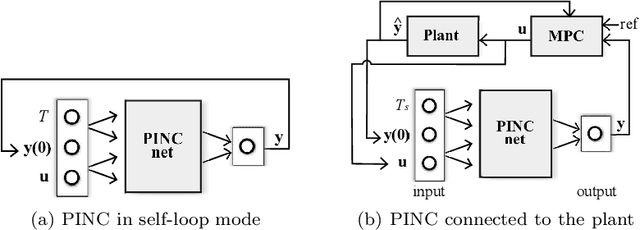
Physics-informed neural networks (PINNs) impose known physical laws into the learning of deep neural networks, making sure they respect the physics of the process while decreasing the demand of labeled data. For systems represented by Ordinary Differential Equations (ODEs), the conventional PINN has a continuous time input variable and outputs the solution of the corresponding ODE. In their original form, PINNs do not allow control inputs neither can they simulate for long-range intervals without serious degradation in their predictions. In this context, this work presents a new framework called Physics-Informed Neural Nets-based Control (PINC), which proposes a novel PINN-based architecture that is amenable to control problems and able to simulate for longer-range time horizons that are not fixed beforehand. First, the network is augmented with new inputs to account for the initial state of the system and the control action. Then, the response over the complete time horizon is split such that each smaller interval constitutes a solution of the ODE conditioned on the fixed values of initial state and control action. The complete response is formed by setting the initial state of the next interval to the terminal state of the previous one. The new methodology enables the optimal control of dynamic systems, making feasible to integrate a priori knowledge from experts and data collected from plants in control applications. We showcase our method in the control of two nonlinear dynamic systems: the Van der Pol oscillator and the four-tank system.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge