Physics-Informed Neural Networks with Skip Connections for Modeling and Control of Gas-Lifted Oil Wells

Neural networks, while powerful, often lack interpretability. Physics-Informed Neural Networks (PINNs) address this limitation by incorporating physics laws into the loss function, making them applicable to solving Ordinary Differential Equations (ODEs) and Partial Differential Equations (PDEs). The recently introduced PINC framework extends PINNs to control applications, allowing for open-ended long-range prediction and control of dynamic systems. In this work, we enhance PINC for modeling highly nonlinear systems such as gas-lifted oil wells. By introducing skip connections in the PINC network and refining certain terms in the ODE, we achieve more accurate gradients during training, resulting in an effective modeling process for the oil well system. Our proposed improved PINC demonstrates superior performance, reducing the validation prediction error by an average of 67% in the oil well application and significantly enhancing gradient flow through the network layers, increasing its magnitude by four orders of magnitude compared to the original PINC. Furthermore, experiments showcase the efficacy of Model Predictive Control (MPC) in regulating the bottom-hole pressure of the oil well using the improved PINC model, even in the presence of noisy measurements.

Adjustment formulas for learning causal steady-state models from closed-loop operational data

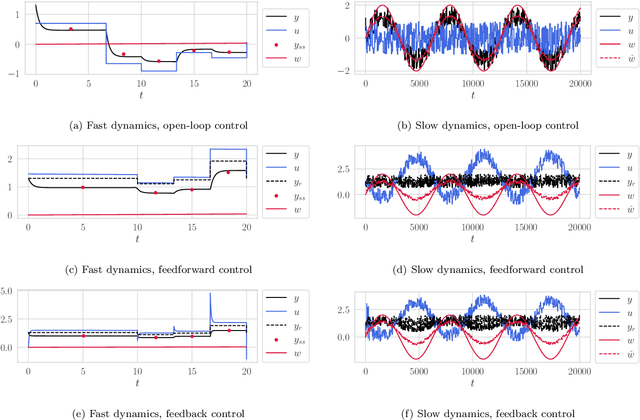
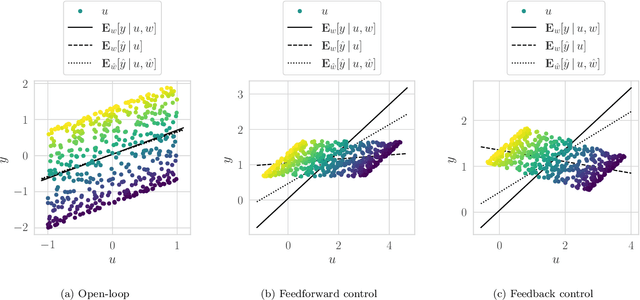
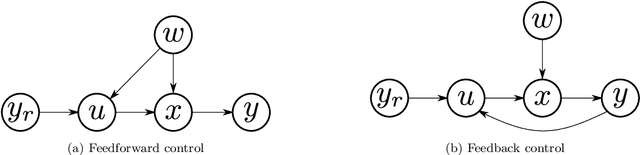
Steady-state models which have been learned from historical operational data may be unfit for model-based optimization unless correlations in the training data which are introduced by control are accounted for. Using recent results from work on structural dynamical causal models, we derive a formula for adjusting for this control confounding, enabling the estimation of a causal steady-state model from closed-loop steady-state data. The formula assumes that the available data have been gathered under some fixed control law. It works by estimating and taking into account the disturbance which the controller is trying to counteract, and enables learning from data gathered under both feedforward and feedback control.