Efficient Federated Learning against Heterogeneous and Non-stationary Client Unavailability

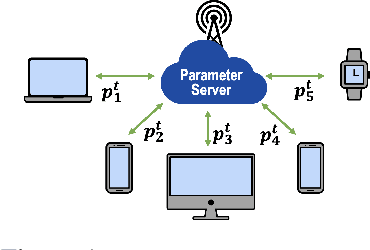
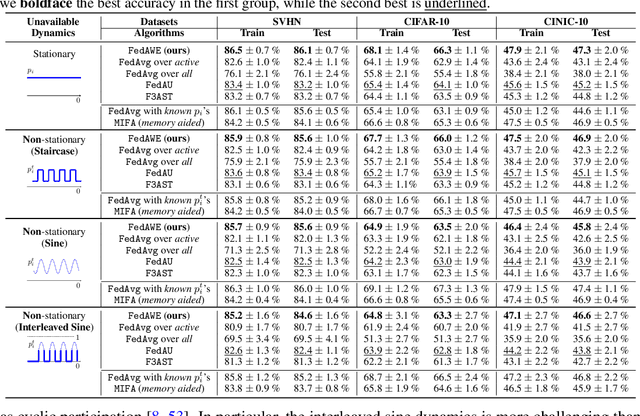
Addressing intermittent client availability is critical for the real-world deployment of federated learning algorithms. Most prior work either overlooks the potential non-stationarity in the dynamics of client unavailability or requires substantial memory/computation overhead. We study federated learning in the presence of heterogeneous and non-stationary client availability, which may occur when the deployment environments are uncertain or the clients are mobile. The impacts of the heterogeneity and non-stationarity in client unavailability can be significant, as we illustrate using FedAvg, the most widely adopted federated learning algorithm. We propose FedAPM, which includes novel algorithmic structures that (i) compensate for missed computations due to unavailability with only $O(1)$ additional memory and computation with respect to standard FedAvg, and (ii) evenly diffuse local updates within the federated learning system through implicit gossiping, despite being agnostic to non-stationary dynamics. We show that FedAPM converges to a stationary point of even non-convex objectives while achieving the desired linear speedup property. We corroborate our analysis with numerical experiments over diversified client unavailability dynamics on real-world data sets.

Fair Concurrent Training of Multiple Models in Federated Learning

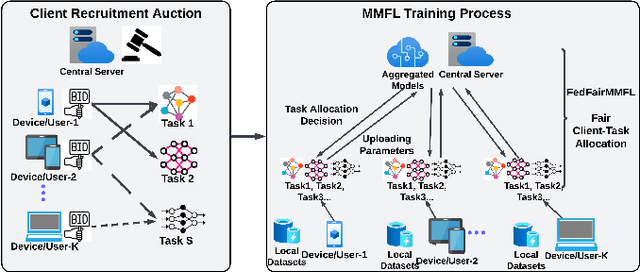
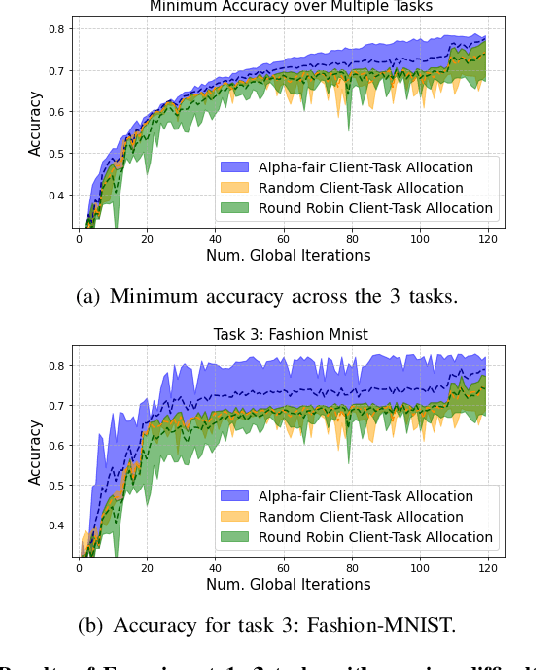
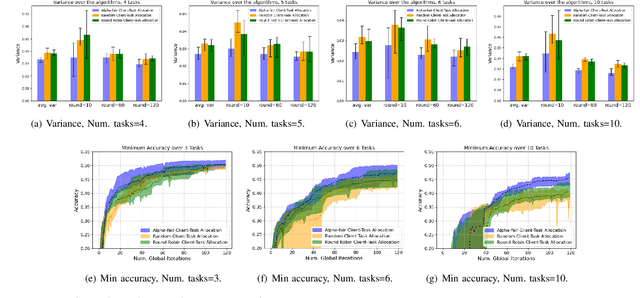
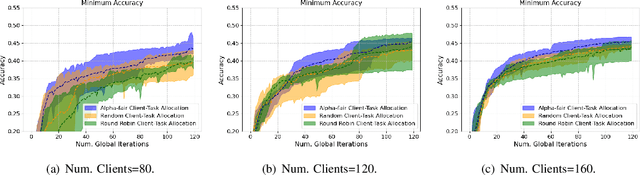
Federated learning (FL) enables collaborative learning across multiple clients. In most FL work, all clients train a single learning task. However, the recent proliferation of FL applications may increasingly require multiple FL tasks to be trained simultaneously, sharing clients' computing and communication resources, which we call Multiple-Model Federated Learning (MMFL). Current MMFL algorithms use naive average-based client-task allocation schemes that can lead to unfair performance when FL tasks have heterogeneous difficulty levels, e.g., tasks with larger models may need more rounds and data to train. Just as naively allocating resources to generic computing jobs with heterogeneous resource needs can lead to unfair outcomes, naive allocation of clients to FL tasks can lead to unfairness, with some tasks having excessively long training times, or lower converged accuracies. Furthermore, in the FL setting, since clients are typically not paid for their training effort, we face a further challenge that some clients may not even be willing to train some tasks, e.g., due to high computational costs, which may exacerbate unfairness in training outcomes across tasks. We address both challenges by firstly designing FedFairMMFL, a difficulty-aware algorithm that dynamically allocates clients to tasks in each training round. We provide guarantees on airness and FedFairMMFL's convergence rate. We then propose a novel auction design that incentivizes clients to train multiple tasks, so as to fairly distribute clients' training efforts across the tasks. We show how our fairness-based learning and incentive mechanisms impact training convergence and finally evaluate our algorithm with multiple sets of learning tasks on real world datasets.

Empowering Federated Learning with Implicit Gossiping: Mitigating Connection Unreliability Amidst Unknown and Arbitrary Dynamics

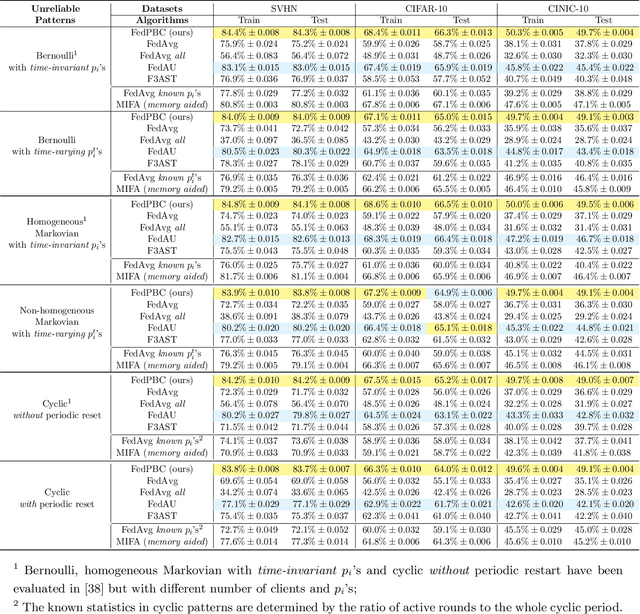
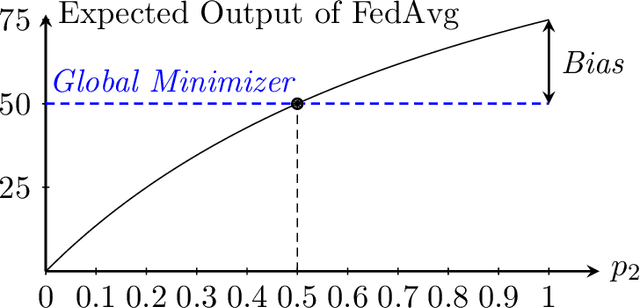
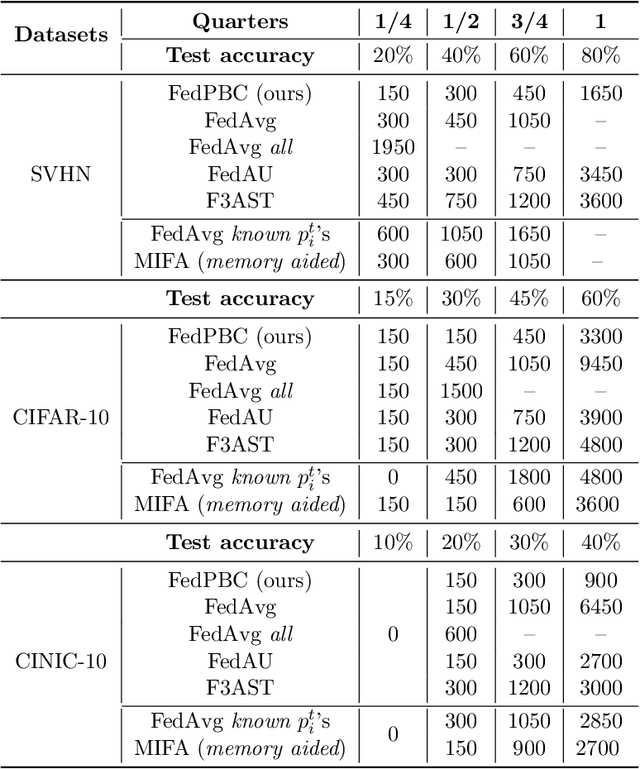
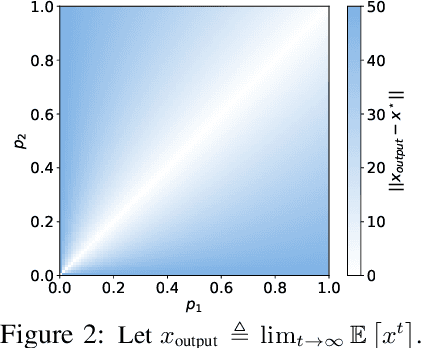
Federated learning is a popular distributed learning approach for training a machine learning model without disclosing raw data. It consists of a parameter server and a possibly large collection of clients (e.g., in cross-device federated learning) that may operate in congested and changing environments. In this paper, we study federated learning in the presence of stochastic and dynamic communication failures wherein the uplink between the parameter server and client $i$ is on with unknown probability $p_i^t$ in round $t$. Furthermore, we allow the dynamics of $p_i^t$ to be arbitrary. We first demonstrate that when the $p_i^t$'s vary across clients, the most widely adopted federated learning algorithm, Federated Average (FedAvg), experiences significant bias. To address this observation, we propose Federated Postponed Broadcast (FedPBC), a simple variant of FedAvg. FedPBC differs from FedAvg in that the parameter server postpones broadcasting the global model till the end of each round. Despite uplink failures, we show that FedPBC converges to a stationary point of the original non-convex objective. On the technical front, postponing the global model broadcasts enables implicit gossiping among the clients with active links in round $t$. Despite the time-varying nature of $p_i^t$, we can bound the perturbation of the global model dynamics using techniques to control gossip-type information mixing errors. Extensive experiments have been conducted on real-world datasets over diversified unreliable uplink patterns to corroborate our analysis.

Towards Bias Correction of FedAvg over Nonuniform and Time-Varying Communications

Federated learning (FL) is a decentralized learning framework wherein a parameter server (PS) and a collection of clients collaboratively train a model via minimizing a global objective. Communication bandwidth is a scarce resource; in each round, the PS aggregates the updates from a subset of clients only. In this paper, we focus on non-convex minimization that is vulnerable to non-uniform and time-varying communication failures between the PS and the clients. Specifically, in each round $t$, the link between the PS and client $i$ is active with probability $p_i^t$, which is $\textit{unknown}$ to both the PS and the clients. This arises when the channel conditions are heterogeneous across clients and are changing over time. We show that when the $p_i^t$'s are not uniform, $\textit{Federated Average}$ (FedAvg) -- the most widely adopted FL algorithm -- fails to minimize the global objective. Observing this, we propose $\textit{Federated Postponed Broadcast}$ (FedPBC) which is a simple variant of FedAvg. It differs from FedAvg in that the PS postpones broadcasting the global model till the end of each round. We show that FedPBC converges to a stationary point of the original objective. The introduced staleness is mild and there is no noticeable slowdown. Both theoretical analysis and numerical results are provided. On the technical front, postponing the global model broadcasts enables implicit gossiping among the clients with active links at round $t$. Despite $p_i^t$'s are time-varying, we are able to bound the perturbation of the global model dynamics via the techniques of controlling the gossip-type information mixing errors.

Robust Regression via Model Based Methods

The mean squared error loss is widely used in many applications, including auto-encoders, multi-target regression, and matrix factorization, to name a few. Despite computational advantages due to its differentiability, it is not robust to outliers. In contrast, l_p norms are known to be robust, but cannot be optimized via, e.g., stochastic gradient descent, as they are non-differentiable. We propose an algorithm inspired by so-called model-based optimization (MBO) [35, 36], which replaces a non-convex objective with a convex model function and alternates between optimizing the model function and updating the solution. We apply this to robust regression, proposing SADM, a stochastic variant of the Online Alternating Direction Method of Multipliers (OADM) [50] to solve the inner optimization in MBO. We show that SADM converges with the rate O(log T/T). Finally, we demonstrate experimentally (a) the robustness of l_p norms to outliers and (b) the efficiency of our proposed model-based algorithms in comparison with gradient methods on autoencoders and multi-target regression.