Armin Moharrer
Robust Regression via Model Based Methods
Jun 29, 2021



Abstract:The mean squared error loss is widely used in many applications, including auto-encoders, multi-target regression, and matrix factorization, to name a few. Despite computational advantages due to its differentiability, it is not robust to outliers. In contrast, l_p norms are known to be robust, but cannot be optimized via, e.g., stochastic gradient descent, as they are non-differentiable. We propose an algorithm inspired by so-called model-based optimization (MBO) [35, 36], which replaces a non-convex objective with a convex model function and alternates between optimizing the model function and updating the solution. We apply this to robust regression, proposing SADM, a stochastic variant of the Online Alternating Direction Method of Multipliers (OADM) [50] to solve the inner optimization in MBO. We show that SADM converges with the rate O(log T/T). Finally, we demonstrate experimentally (a) the robustness of l_p norms to outliers and (b) the efficiency of our proposed model-based algorithms in comparison with gradient methods on autoencoders and multi-target regression.
Submodular Maximization via Taylor Series Approximation
Jan 19, 2021
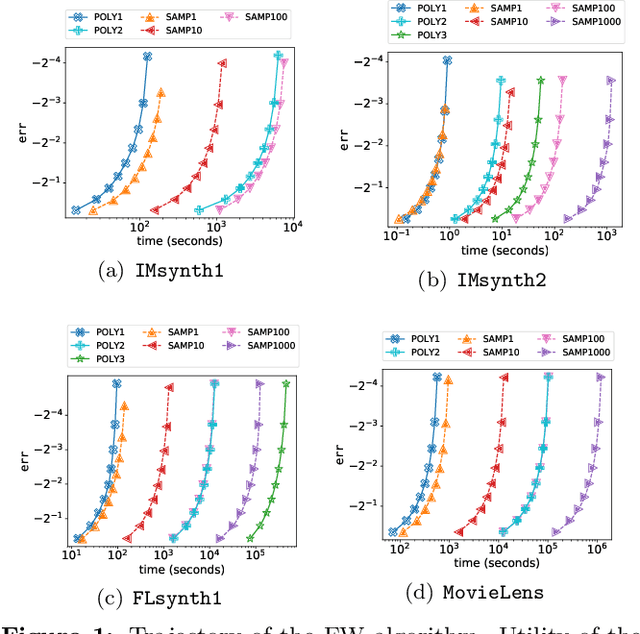

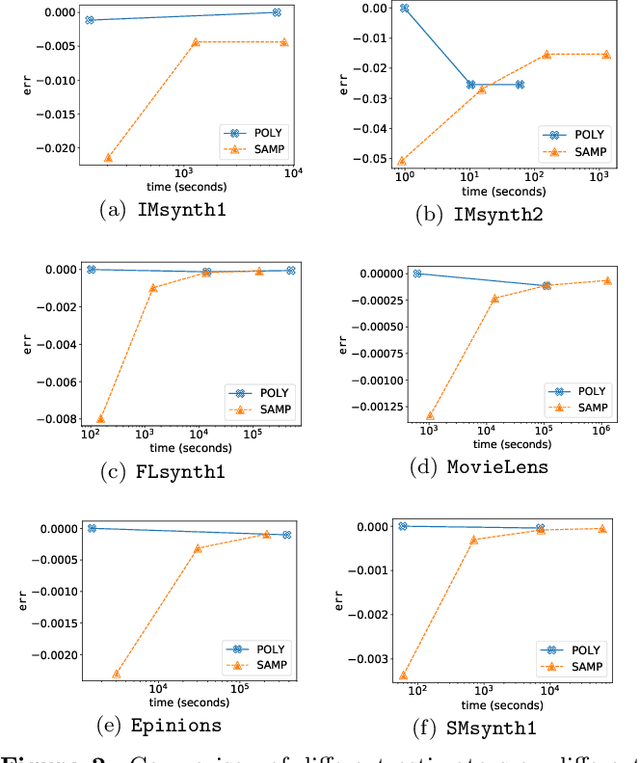
Abstract:We study submodular maximization problems with matroid constraints, in particular, problems where the objective can be expressed via compositions of analytic and multilinear functions. We show that for functions of this form, the so-called continuous greedy algorithm attains a ratio arbitrarily close to $(1-1/e) \approx 0.63$ using a deterministic estimation via Taylor series approximation. This drastically reduces execution time over prior art that uses sampling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge