Learning Set Functions with Implicit Differentiation

Ou et al. (2022) introduce the problem of learning set functions from data generated by a so-called optimal subset oracle. Their approach approximates the underlying utility function with an energy-based model, whose parameters are estimated via mean-field variational inference. Ou et al. (2022) show this reduces to fixed point iterations; however, as the number of iterations increases, automatic differentiation quickly becomes computationally prohibitive due to the size of the Jacobians that are stacked during backpropagation. We address this challenge with implicit differentiation and examine the convergence conditions for the fixed-point iterations. We empirically demonstrate the efficiency of our method on synthetic and real-world subset selection applications including product recommendation, set anomaly detection and compound selection tasks.

Online Submodular Maximization via Online Convex Optimization

We study monotone submodular maximization under general matroid constraints in the online setting. We prove that online optimization of a large class of submodular functions, namely, weighted threshold potential functions, reduces to online convex optimization (OCO). This is precisely because functions in this class admit a concave relaxation; as a result, OCO policies, coupled with an appropriate rounding scheme, can be used to achieve sublinear regret in the combinatorial setting. We show that our reduction extends to many different versions of the online learning problem, including the dynamic regret, bandit, and optimistic-learning settings.

Stochastic Submodular Maximization via Polynomial Estimators

In this paper, we study stochastic submodular maximization problems with general matroid constraints, that naturally arise in online learning, team formation, facility location, influence maximization, active learning and sensing objective functions. In other words, we focus on maximizing submodular functions that are defined as expectations over a class of submodular functions with an unknown distribution. We show that for monotone functions of this form, the stochastic continuous greedy algorithm attains an approximation ratio (in expectation) arbitrarily close to $(1-1/e) \approx 63\%$ using a polynomial estimation of the gradient. We argue that using this polynomial estimator instead of the prior art that uses sampling eliminates a source of randomness and experimentally reduces execution time.

Submodular Maximization via Taylor Series Approximation

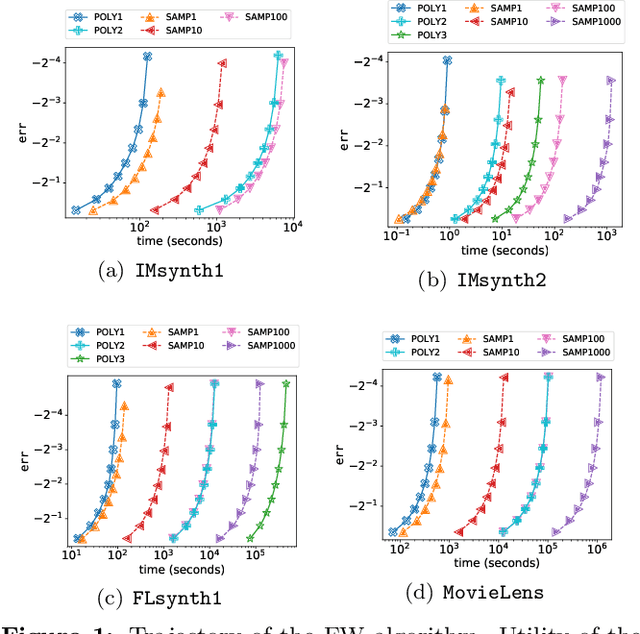
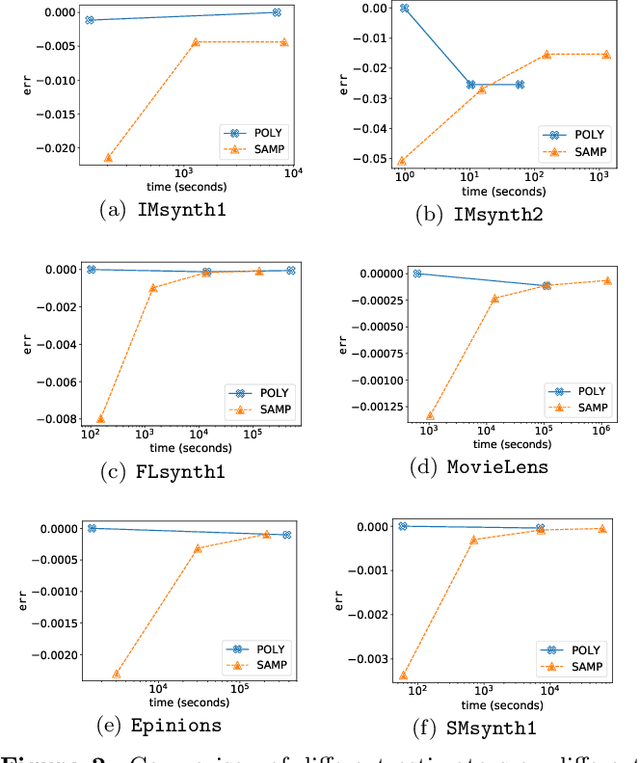
We study submodular maximization problems with matroid constraints, in particular, problems where the objective can be expressed via compositions of analytic and multilinear functions. We show that for functions of this form, the so-called continuous greedy algorithm attains a ratio arbitrarily close to $(1-1/e) \approx 0.63$ using a deterministic estimation via Taylor series approximation. This drastically reduces execution time over prior art that uses sampling.