Submodular Maximization via Taylor Series Approximation

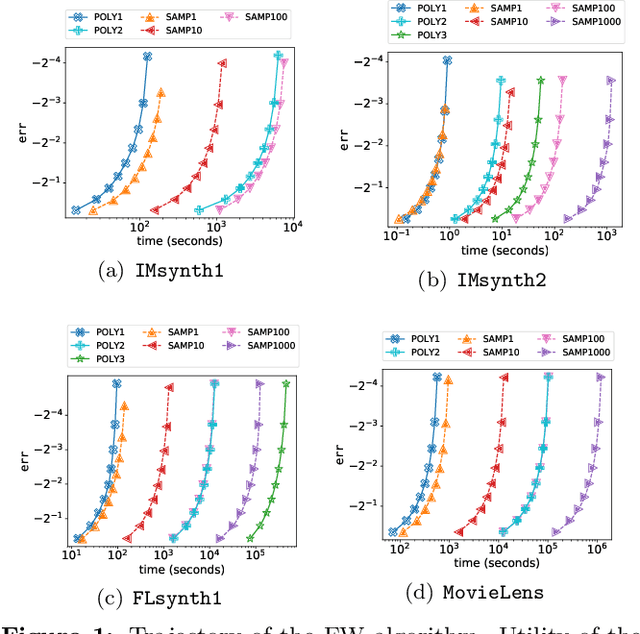
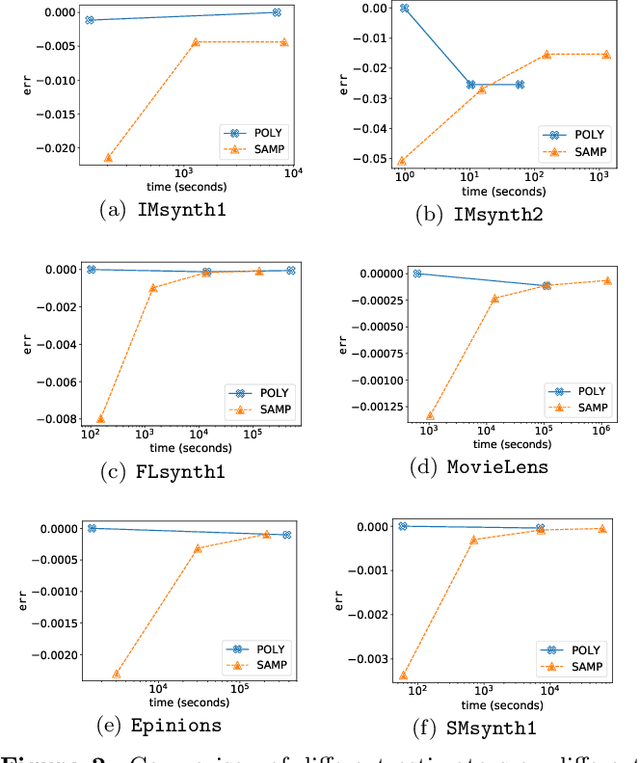
We study submodular maximization problems with matroid constraints, in particular, problems where the objective can be expressed via compositions of analytic and multilinear functions. We show that for functions of this form, the so-called continuous greedy algorithm attains a ratio arbitrarily close to $(1-1/e) \approx 0.63$ using a deterministic estimation via Taylor series approximation. This drastically reduces execution time over prior art that uses sampling.