Efficient Federated Learning against Heterogeneous and Non-stationary Client Unavailability

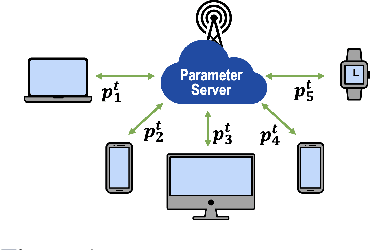
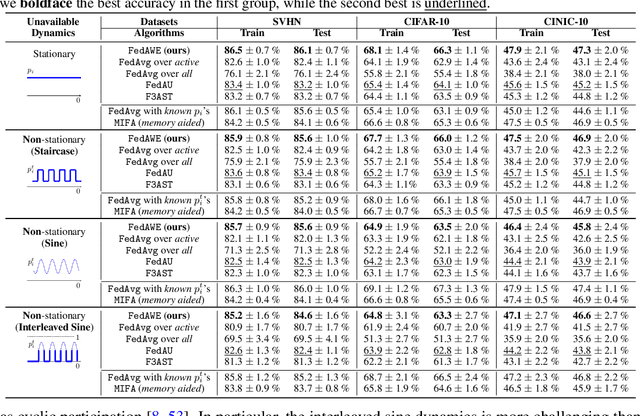
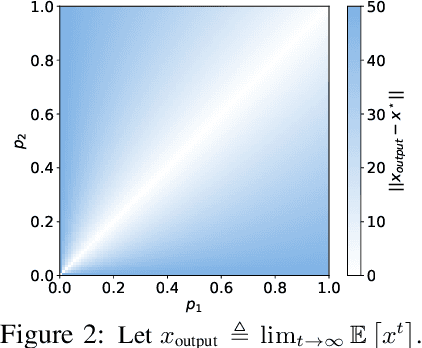
Addressing intermittent client availability is critical for the real-world deployment of federated learning algorithms. Most prior work either overlooks the potential non-stationarity in the dynamics of client unavailability or requires substantial memory/computation overhead. We study federated learning in the presence of heterogeneous and non-stationary client availability, which may occur when the deployment environments are uncertain or the clients are mobile. The impacts of the heterogeneity and non-stationarity in client unavailability can be significant, as we illustrate using FedAvg, the most widely adopted federated learning algorithm. We propose FedAPM, which includes novel algorithmic structures that (i) compensate for missed computations due to unavailability with only $O(1)$ additional memory and computation with respect to standard FedAvg, and (ii) evenly diffuse local updates within the federated learning system through implicit gossiping, despite being agnostic to non-stationary dynamics. We show that FedAPM converges to a stationary point of even non-convex objectives while achieving the desired linear speedup property. We corroborate our analysis with numerical experiments over diversified client unavailability dynamics on real-world data sets.

Active Use of Latent Constituency Representation in both Humans and Large Language Models

Understanding how sentences are internally represented in the human brain, as well as in large language models (LLMs) such as ChatGPT, is a major challenge for cognitive science. Classic linguistic theories propose that the brain represents a sentence by parsing it into hierarchically organized constituents. In contrast, LLMs do not explicitly parse linguistic constituents and their latent representations remains poorly explained. Here, we demonstrate that humans and LLMs construct similar latent representations of hierarchical linguistic constituents by analyzing their behaviors during a novel one-shot learning task, in which they infer which words should be deleted from a sentence. Both humans and LLMs tend to delete a constituent, instead of a nonconstituent word string. In contrast, a naive sequence processing model that has access to word properties and ordinal positions does not show this property. Based on the word deletion behaviors, we can reconstruct the latent constituency tree representation of a sentence for both humans and LLMs. These results demonstrate that a latent tree-structured constituency representation can emerge in both the human brain and LLMs.

Empowering Federated Learning with Implicit Gossiping: Mitigating Connection Unreliability Amidst Unknown and Arbitrary Dynamics

Federated learning is a popular distributed learning approach for training a machine learning model without disclosing raw data. It consists of a parameter server and a possibly large collection of clients (e.g., in cross-device federated learning) that may operate in congested and changing environments. In this paper, we study federated learning in the presence of stochastic and dynamic communication failures wherein the uplink between the parameter server and client $i$ is on with unknown probability $p_i^t$ in round $t$. Furthermore, we allow the dynamics of $p_i^t$ to be arbitrary. We first demonstrate that when the $p_i^t$'s vary across clients, the most widely adopted federated learning algorithm, Federated Average (FedAvg), experiences significant bias. To address this observation, we propose Federated Postponed Broadcast (FedPBC), a simple variant of FedAvg. FedPBC differs from FedAvg in that the parameter server postpones broadcasting the global model till the end of each round. Despite uplink failures, we show that FedPBC converges to a stationary point of the original non-convex objective. On the technical front, postponing the global model broadcasts enables implicit gossiping among the clients with active links in round $t$. Despite the time-varying nature of $p_i^t$, we can bound the perturbation of the global model dynamics using techniques to control gossip-type information mixing errors. Extensive experiments have been conducted on real-world datasets over diversified unreliable uplink patterns to corroborate our analysis.

Towards Bias Correction of FedAvg over Nonuniform and Time-Varying Communications

Federated learning (FL) is a decentralized learning framework wherein a parameter server (PS) and a collection of clients collaboratively train a model via minimizing a global objective. Communication bandwidth is a scarce resource; in each round, the PS aggregates the updates from a subset of clients only. In this paper, we focus on non-convex minimization that is vulnerable to non-uniform and time-varying communication failures between the PS and the clients. Specifically, in each round $t$, the link between the PS and client $i$ is active with probability $p_i^t$, which is $\textit{unknown}$ to both the PS and the clients. This arises when the channel conditions are heterogeneous across clients and are changing over time. We show that when the $p_i^t$'s are not uniform, $\textit{Federated Average}$ (FedAvg) -- the most widely adopted FL algorithm -- fails to minimize the global objective. Observing this, we propose $\textit{Federated Postponed Broadcast}$ (FedPBC) which is a simple variant of FedAvg. It differs from FedAvg in that the PS postpones broadcasting the global model till the end of each round. We show that FedPBC converges to a stationary point of the original objective. The introduced staleness is mild and there is no noticeable slowdown. Both theoretical analysis and numerical results are provided. On the technical front, postponing the global model broadcasts enables implicit gossiping among the clients with active links at round $t$. Despite $p_i^t$'s are time-varying, we are able to bound the perturbation of the global model dynamics via the techniques of controlling the gossip-type information mixing errors.

$β$-Stochastic Sign SGD: A Byzantine Resilient and Differentially Private Gradient Compressor for Federated Learning

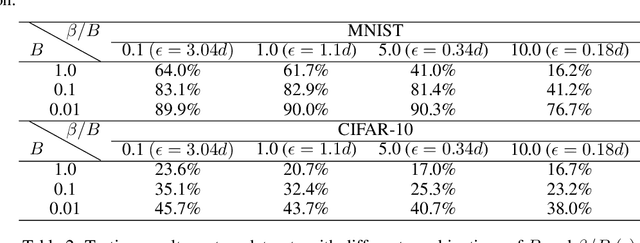
Federated Learning (FL) is a nascent privacy-preserving learning framework under which the local data of participating clients is kept locally throughout model training. Scarce communication resources and data heterogeneity are two defining characteristics of FL. Besides, a FL system is often implemented in a harsh environment -- leaving the clients vulnerable to Byzantine attacks. To the best of our knowledge, no gradient compressors simultaneously achieve quantitative Byzantine resilience and privacy preservation. In this paper, we fill this gap via revisiting the stochastic sign SGD \cite{jin 2020}. We propose $\beta$-stochastic sign SGD, which contains a gradient compressor that encodes a client's gradient information in sign bits subject to the privacy budget $\beta>0$. We show that as long as $\beta>0$, $\beta$-stochastic sign SGD converges in the presence of partial client participation and mobile Byzantine faults, showing that it achieves quantifiable Byzantine-resilience and differential privacy simultaneously. In sharp contrast, when $\beta=0$, the compressor is not differentially private. Notably, for the special case when each of the stochastic gradients involved is bounded with known bounds, our gradient compressor with $\beta=0$ coincides with the compressor proposed in \cite{jin 2020}. As a byproduct, we show that when the clients report sign messages, the popular information aggregation rules simple mean, trimmed mean, median and majority vote are identical in terms of the output signs. Our theories are corroborated by experiments on MNIST and CIFAR-10 datasets.

An Empirical Analysis of Approximation Algorithms for the Euclidean Traveling Salesman Problem

With applications to many disciplines, the traveling salesman problem (TSP) is a classical computer science optimization problem with applications to industrial engineering, theoretical computer science, bioinformatics, and several other disciplines. In recent years, there have been a plethora of novel approaches for approximate solutions ranging from simplistic greedy to cooperative distributed algorithms derived from artificial intelligence. In this paper, we perform an evaluation and analysis of cornerstone algorithms for the Euclidean TSP. We evaluate greedy, 2-opt, and genetic algorithms. We use several datasets as input for the algorithms including a small dataset, a mediumsized dataset representing cities in the United States, and a synthetic dataset consisting of 200 cities to test algorithm scalability. We discover that the greedy and 2-opt algorithms efficiently calculate solutions for smaller datasets. Genetic algorithm has the best performance for optimality for medium to large datasets, but generally have longer runtime. Our implementations is public available.