$β$-Stochastic Sign SGD: A Byzantine Resilient and Differentially Private Gradient Compressor for Federated Learning

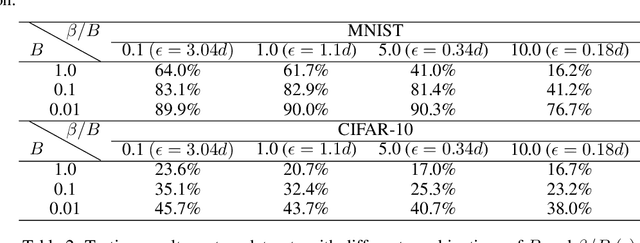
Federated Learning (FL) is a nascent privacy-preserving learning framework under which the local data of participating clients is kept locally throughout model training. Scarce communication resources and data heterogeneity are two defining characteristics of FL. Besides, a FL system is often implemented in a harsh environment -- leaving the clients vulnerable to Byzantine attacks. To the best of our knowledge, no gradient compressors simultaneously achieve quantitative Byzantine resilience and privacy preservation. In this paper, we fill this gap via revisiting the stochastic sign SGD \cite{jin 2020}. We propose $\beta$-stochastic sign SGD, which contains a gradient compressor that encodes a client's gradient information in sign bits subject to the privacy budget $\beta>0$. We show that as long as $\beta>0$, $\beta$-stochastic sign SGD converges in the presence of partial client participation and mobile Byzantine faults, showing that it achieves quantifiable Byzantine-resilience and differential privacy simultaneously. In sharp contrast, when $\beta=0$, the compressor is not differentially private. Notably, for the special case when each of the stochastic gradients involved is bounded with known bounds, our gradient compressor with $\beta=0$ coincides with the compressor proposed in \cite{jin 2020}. As a byproduct, we show that when the clients report sign messages, the popular information aggregation rules simple mean, trimmed mean, median and majority vote are identical in terms of the output signs. Our theories are corroborated by experiments on MNIST and CIFAR-10 datasets.