Point Normal Orientation and Surface Reconstruction by Incorporating Isovalue Constraints to Poisson Equation

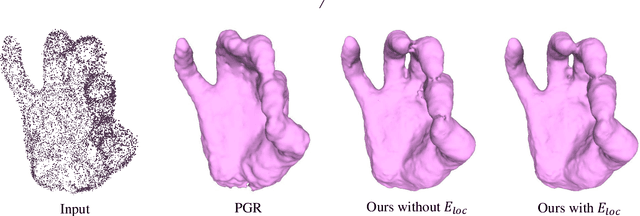
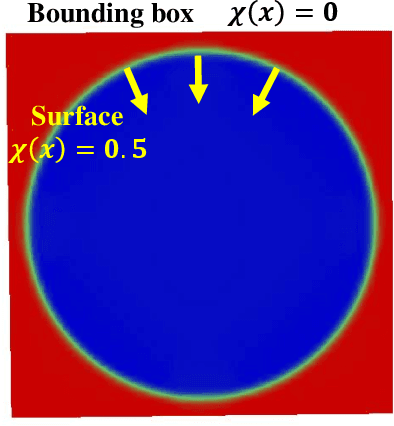
Oriented normals are common pre-requisites for many geometric algorithms based on point clouds, such as Poisson surface reconstruction. However, it is not trivial to obtain a consistent orientation. In this work, we bridge orientation and reconstruction in implicit space and propose a novel approach to orient point clouds by incorporating isovalue constraints to the Poisson equation. Feeding a well-oriented point cloud into a reconstruction approach, the indicator function values of the sample points should be close to the isovalue. Based on this observation and the Poisson equation, we propose an optimization formulation that combines isovalue constraints with local consistency requirements for normals. We optimize normals and implicit functions simultaneously and solve for a globally consistent orientation. Owing to the sparsity of the linear system, an average laptop can be used to run our method within reasonable time. Experiments show that our method can achieve high performance in non-uniform and noisy data and manage varying sampling densities, artifacts, multiple connected components, and nested surfaces.

Compact and Robust Deep Learning Architecture for Fluorescence Lifetime Imaging and FPGA Implementation

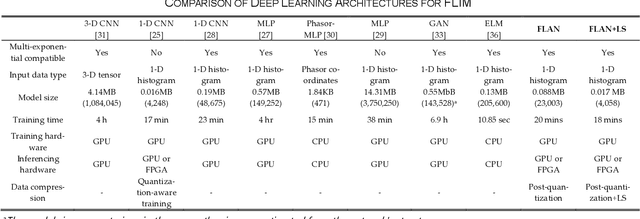
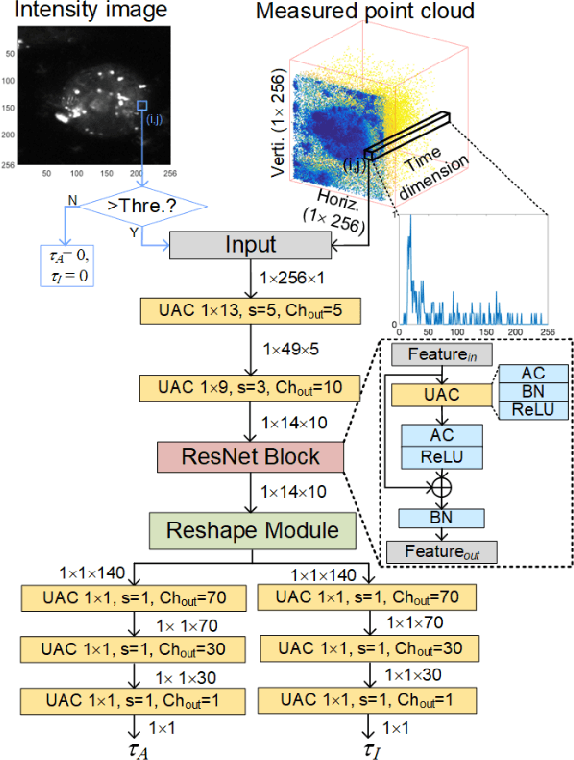
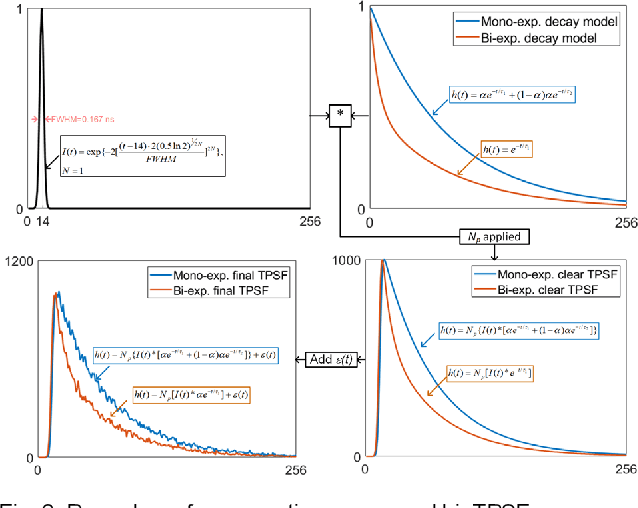
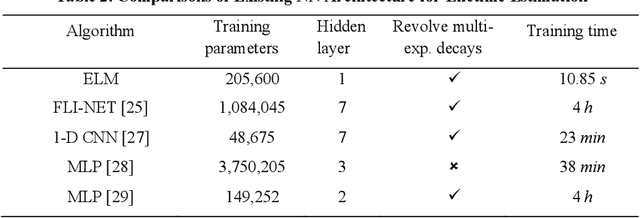
This paper reported a bespoke adder-based deep learning network for time-domain fluorescence lifetime imaging (FLIM). By leveraging the l1-norm extraction method, we propose a 1-D Fluorescence Lifetime AdderNet (FLAN) without multiplication-based convolutions to reduce the computational complexity. Further, we compressed fluorescence decays in temporal dimension using a log-scale merging technique to discard redundant temporal information derived as log-scaling FLAN (FLAN+LS). FLAN+LS achieves 0.11 and 0.23 compression ratios compared with FLAN and a conventional 1-D convolutional neural network (1-D CNN) while maintaining high accuracy in retrieving lifetimes. We extensively evaluated FLAN and FLAN+LS using synthetic and real data. A traditional fitting method and other non-fitting, high-accuracy algorithms were compared with our networks for synthetic data. Our networks attained a minor reconstruction error in different photon-count scenarios. For real data, we used fluorescent beads' data acquired by a confocal microscope to validate the effectiveness of real fluorophores, and our networks can differentiate beads with different lifetimes. Additionally, we implemented the network architecture on a field-programmable gate array (FPGA) with a post-quantization technique to shorten the bit-width, thereby improving computing efficiency. FLAN+LS on hardware achieves the highest computing efficiency compared to 1-D CNN and FLAN. We also discussed the applicability of our network and hardware architecture for other time-resolved biomedical applications using photon-efficient, time-resolved sensors.

Fast fluorescence lifetime imaging analysis via extreme learning machine

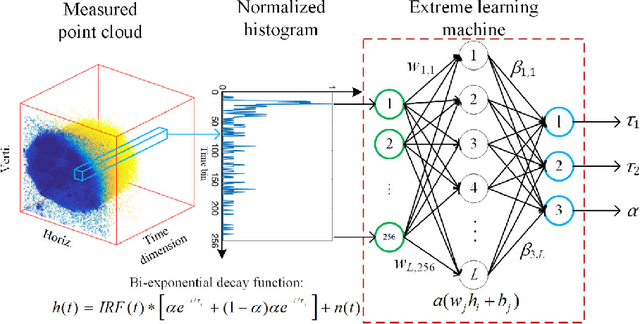
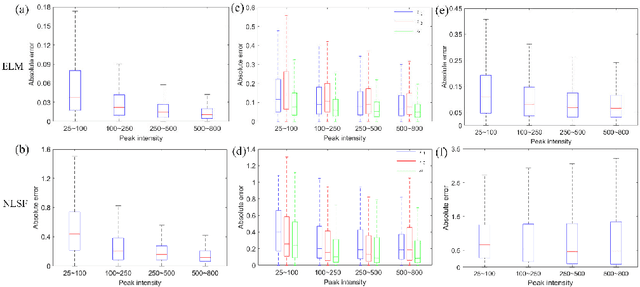
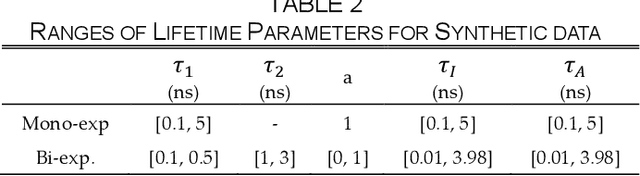
We present a fast and accurate analytical method for fluorescence lifetime imaging microscopy (FLIM) using the extreme learning machine (ELM). We used extensive metrics to evaluate ELM and existing algorithms. First, we compared these algorithms using synthetic datasets. Results indicate that ELM can obtain higher fidelity, even in low-photon conditions. Afterwards, we used ELM to retrieve lifetime components from human prostate cancer cells loaded with gold nanosensors, showing that ELM also outperforms the iterative fitting and non-fitting algorithms. By comparing ELM with a computational efficient neural network, ELM achieves comparable accuracy with less training and inference time. As there is no back-propagation process for ELM during the training phase, the training speed is much higher than existing neural network approaches. The proposed strategy is promising for edge computing with online training.

Learning Modified Indicator Functions for Surface Reconstruction

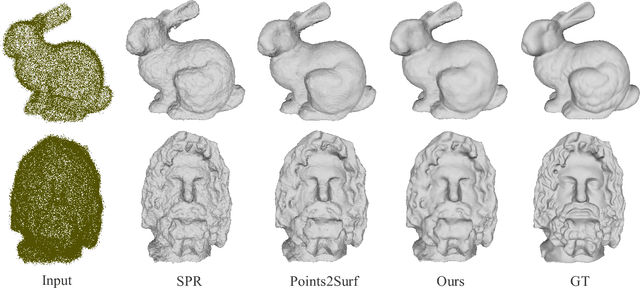
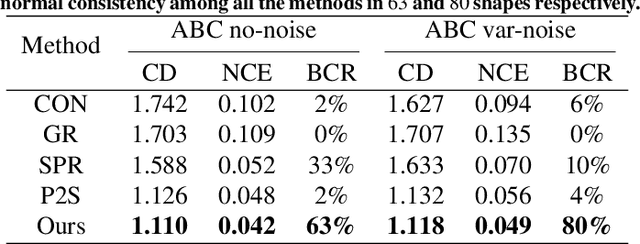
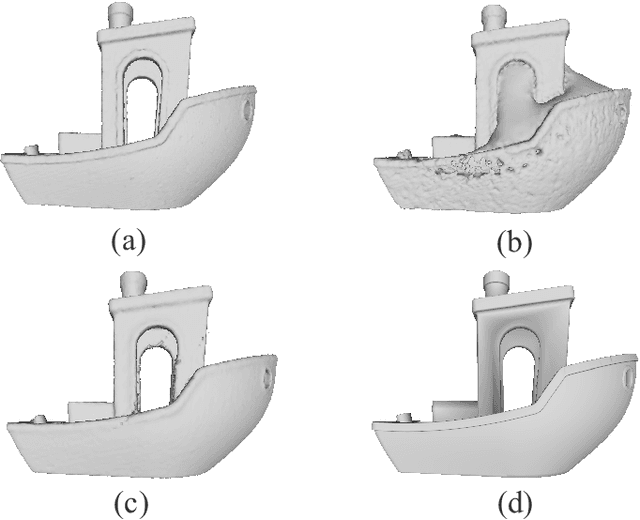
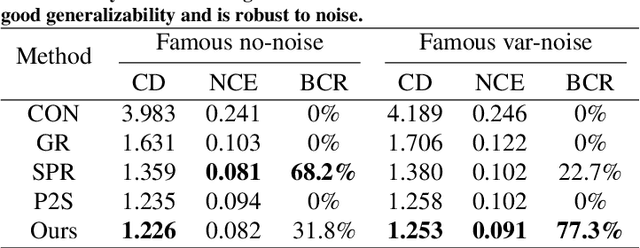
Surface reconstruction is a fundamental problem in 3D graphics. In this paper, we propose a learning-based approach for implicit surface reconstruction from raw point clouds without normals. Our method is inspired by Gauss Lemma in potential energy theory, which gives an explicit integral formula for the indicator functions. We design a novel deep neural network to perform surface integral and learn the modified indicator functions from un-oriented and noisy point clouds. We concatenate features with different scales for accurate point-wise contributions to the integral. Moreover, we propose a novel Surface Element Feature Extractor to learn local shape properties. Experiments show that our method generates smooth surfaces with high normal consistency from point clouds with different noise scales and achieves state-of-the-art reconstruction performance compared with current data-driven and non-data-driven approaches.