Point Normal Orientation and Surface Reconstruction by Incorporating Isovalue Constraints to Poisson Equation
Paper and Code
Sep 30, 2022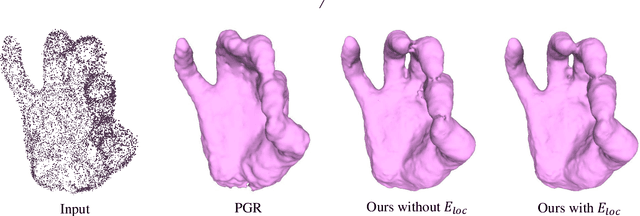

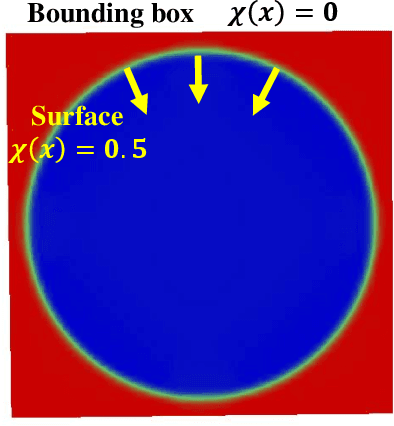

Oriented normals are common pre-requisites for many geometric algorithms based on point clouds, such as Poisson surface reconstruction. However, it is not trivial to obtain a consistent orientation. In this work, we bridge orientation and reconstruction in implicit space and propose a novel approach to orient point clouds by incorporating isovalue constraints to the Poisson equation. Feeding a well-oriented point cloud into a reconstruction approach, the indicator function values of the sample points should be close to the isovalue. Based on this observation and the Poisson equation, we propose an optimization formulation that combines isovalue constraints with local consistency requirements for normals. We optimize normals and implicit functions simultaneously and solve for a globally consistent orientation. Owing to the sparsity of the linear system, an average laptop can be used to run our method within reasonable time. Experiments show that our method can achieve high performance in non-uniform and noisy data and manage varying sampling densities, artifacts, multiple connected components, and nested surfaces.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge